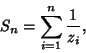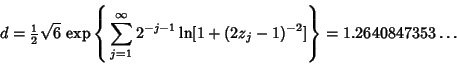| 释义 |
Quadratic RecurrenceN.B. A detailed on-line essay by S. Finchwas the starting point for this entry.
A quadratic recurrence is a Recurrence Relation on a Sequence of numbers  expressing expressing  as asecond degree polynomial in as asecond degree polynomial in  with with  . For example, . For example,
 | (1) |
 | (2) |
 , which has solution , which has solution  . Another example is the number of ``strongly'' binary trees of height . Another example is the number of ``strongly'' binary trees of height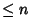 , given by , given by
 | (3) |
 . This has solution . This has solution
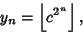 | (4) |
 | (5) |
 is the Floor Function (Aho and Sloane 1973). A third example is the closest strict underapproximation ofthe number 1, is the Floor Function (Aho and Sloane 1973). A third example is the closest strict underapproximation ofthe number 1,
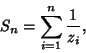 | (6) |
 are integers. The solution is given by the recurrence are integers. The solution is given by the recurrence
 | (7) |
 . This has a closed solution as . This has a closed solution as
 | (8) |
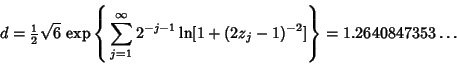 | (9) |
 | (10) |
 used to generate the Mandelbrot Set.See also Mandelbrot Set, Recurrence Relation used to generate the Mandelbrot Set.See also Mandelbrot Set, Recurrence Relation
References
Aho, A. V. and Sloane, N. J. A. ``Some Doubly Exponential Sequences.'' Fib. Quart. 11, 429-437, 1973.Finch, S. ``Favorite Mathematical Constants.'' http://www.mathsoft.com/asolve/constant/quad/quad.html |
![]() expressing
expressing ![]() as asecond degree polynomial in
as asecond degree polynomial in ![]() with
with ![]() . For example,
. For example,