Fejes Tóth's Problem
How can ![]() points be distributed on a Unit Sphere such that they maximize the minimum distance between any pair ofpoints? In 1943, Fejes Tóth proved that for
points be distributed on a Unit Sphere such that they maximize the minimum distance between any pair ofpoints? In 1943, Fejes Tóth proved that for ![]() points, there always exist two points whosedistance
points, there always exist two points whosedistance ![]() is
is
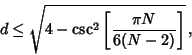
and that the limit is exact for
For two points, the points should be at opposite ends of a Diameter. Forfour points, they should be placed at the Vertices of an inscribed Tetrahedron.There is no best solution for five points since the distance cannot be reduced below that for six points. For six points,they should be placed at the Vertices of an inscribed Octahedron. For seven points,the best solution is four equilateral spherical triangles with angles of 80°. For eight points, the best dispersalis not the Vertices of the inscribed Cube, but of a square Antiprismwith equal Edges. The solution for nine points is eight equilateral spherical triangles withangles of ![]() . For 12 points, the solution is an inscribed Icosahedron.
. For 12 points, the solution is an inscribed Icosahedron.
The general problem has not been solved.
See also Thomson Problem
References
Ogilvy, C. S. Excursions in Mathematics. New York: Dover, p. 99, 1994. Ogilvy, C. S. Solved by L. Moser. ``Minimal Configuration of Five Points on a Sphere.'' Problem E946. Amer. Math. Monthly 58, 592, 1951. Schütte, K. and van der Waerden, B. L. ``Auf welcher Kügel haben 5, 6, 7, 8 oder 9 Pünkte mit Mindestabstand Eins Platz?'' Math. Ann. 123, 96-124, 1951. Whyte, L. L. ``Unique Arrangement of Points on a Sphere.'' Amer. Math. Monthly 59, 606-611, 1952.
- Milne's Method
- Milnor's Conjecture
- Milnor's Theorem
- Minimal Cover
- Minimal Discriminant
- Minimal Matrix
- Minimal Residue
- Minimal Set
- Minimal Surface
- Minimax Approximation
- Minimax Polynomial
- Minimax Theorem
- Minimum
- Minkowski-Bouligand Dimension
- Minkowski Convex Body Theorem
- Minkowski Geometry
- Minkowski-Hlawka Theorem
- Minkowski Integral Inequality
- Minkowski Measure
- Minkowski Metric
- Minkowski Sausage
- Minkowski Space
- Minkowski Sum
- Minkowski Sum Inequality
- Minor