“Pentagon”的概念、定义、习题解题方法及翻译-数学辞典

单词

Pentagon

释义

Pentagon

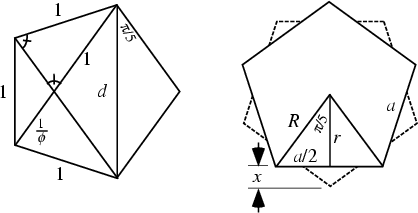
The regular convex 5-gon is called the pentagon. By Similar Triangles in the figure on theleft,

(1)

where

is the diagonal distance. But the dashed vertical line connecting two nonadjacent Vertices is the same length as the diagonal one, so

(2)

(3)

Solving the Quadratic Equation gives

(4)

and taking the plus sign gives the Golden Ratio

(5)

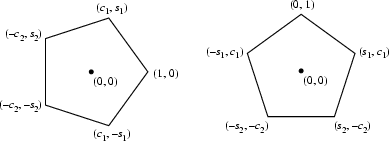
The coordinates of the Vertices relative to the center of the pentagon with unit sides are given asshown in the above figure, with

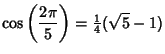			(6)
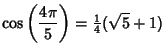			(7)
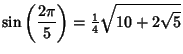			(8)
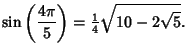			(9)

For a regular Polygon, the Circumradius, Inradius, Sagitta,and Area are given by

			(10)
			(11)
			(12)
			(13)

Plugging in

gives

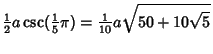			(14)
			(15)
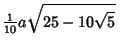			(16)
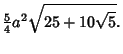			(17)

Five pentagons can be arranged around an identical pentagon to form the first iteration of the ``Pentaflake,''which itself has the shape of a pentagon with five triangular wedges removed. For a pentagon of side length 1,the first ring of pentagons has centers at radius , the second ring at , and the th at.

In proposition IV.11, Euclid showed how to inscribe a regular pentagon in a Ptolemy also gave a Ruler and Compass construction for the pentagon in his epoch-making work The Almagest. While Ptolemy's construction has a Simplicity of 16, a Geometric Construction using CarlyleCircles can be made with Geometrography symbol , which hasSimplicity 15 (De Temple 1991).

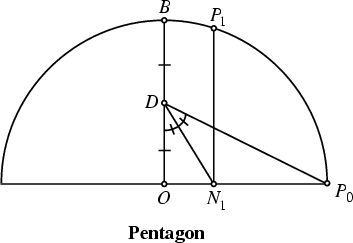
The following elegant construction for the pentagon is due to Richmond (1893). Given a point, a Circle may beconstructed of any desired Radius, and a Diameter drawn through the center. Call the center , and the rightend of the Diameter . The Diameter Perpendicular to the original Diameter may be constructedby finding the Perpendicular Bisector. Call the upper endpoint of this Perpendicular Diameter . Forthe pentagon, find the Midpoint of and call it . Draw , and Bisect , calling the intersection point with . Draw Parallel to , and the first two points ofthe pentagon are and (Coxeter 1969).

Madachy (1979) illustrates how to construct a pentagon by folding and knotting a strip of paper.

See also Cyclic Pentagon, Decagon, Dissection, Five Disks Problem, Home Plate,Pentaflake, Pentagram, Polygon, Trigonometry Values Pi/5

References

Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, pp. 95-96, 1987.

Coxeter, H. S. M. Introduction to Geometry, 2nd ed. New York: Wiley, pp. 26-28, 1969.

De Temple, D. W. ``Carlyle Circles and the Lemoine Simplicity of Polygonal Constructions.'' Amer. Math. Monthly 98, 97-108, 1991.

Dixon, R. Mathographics. New York: Dover, p. 17, 1991.

Dudeney, H. E. Amusements in Mathematics. New York: Dover, p. 38, 1970.

Madachy, J. S. Madachy's Mathematical Recreations. New York: Dover, p. 59, 1979.

Pappas, T. ``The Pentagon, the Pentagram & the Golden Triangle.'' The Joy of Mathematics. San Carlos, CA: Wide World Publ./Tetra, pp. 188-189, 1989.

Richmond, H. W. ``A Construction for a Regular Polygon of Seventeen Sides.'' Quart. J. Pure Appl. Math. 26, 206-207, 1893.

Wantzel, M. L. ``Recherches sur les moyens de reconnaître si un Problème de Géométrie peut se résoudre avec la règle et le compas.'' J. Math. pures appliq. 1, 366-372, 1836.

随便看

数学辞典收录了8975条数学词条，基本涵盖了常用数学知识及数学英语单词词组的翻译及用法，是数学学习的有利工具。