| 释义 |
Linear TransformationAn 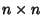 Matrix Matrix  is a linear transformation (linear Map) Iff, for every pair of is a linear transformation (linear Map) Iff, for every pair of -Vectors -Vectors 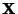 and and  and every Scalar and every Scalar 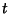 , ,
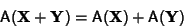 | (1) |
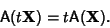 | (2) |
Consider the 2-D transformation
Rescale by defining  and and 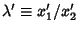 , then the above equations become , then the above equations become
 | (5) |
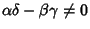 and and  , , 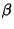 , , 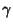 and and 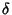 are defined in terms of the oldconstants. Solving for are defined in terms of the oldconstants. Solving for  gives gives
 | (6) |
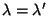 to obtain to obtain
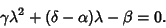 | (7) |
| variables | type | 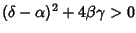 | Hyperbolic Fixed Point | 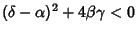 | Elliptic Fixed Point | 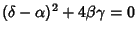 | Parabolic Fixed Point |
References
Woods, F. S. Higher Geometry: An Introduction to Advanced Methods in Analytic Geometry. New York: Dover, pp. 13-15, 1961. |
![]() Matrix
Matrix ![]() is a linear transformation (linear Map) Iff, for every pair of
is a linear transformation (linear Map) Iff, for every pair of![]() -Vectors
-Vectors ![]() and
and ![]() and every Scalar
and every Scalar ![]() ,
,