Lucas Sequence
Let 
, 
be Positive Integers. The Roots of
 | (1) |
 |  |  | (2) |
 | |  | (3) |
where
 | (4) |
 |  |  | (5) |
 | |  | (6) |
 | |  | (7) |
Then define
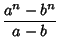 | |  | (8) |
 | |  | (9) |
The first few values are therefore
 | |  | (10) |
 | |  | (11) |
 | |  | (12) |
 | |  | (13) |
The sequences
 | |  | (14) |
 | |  | (15) |
are called Lucas sequences, where the definition is usually extended to include
 | (16) |
For 
, the 
are the Fibonacci Numbers and 
are the LucasNumbers. For 
, the Pell Numbers and Pell-Lucas numbers are obtained. 
produces the Jacobsthal Numbers and Pell-Jacobsthal Numbers.
The Lucas sequences satisfy the general Recurrence Relations
 | |  | |
|  | ||
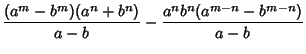|  | (17) | |
 | |  | |
|  | ||
|  | (18) |
Taking
then gives | |  | (19) |
 | |  | (20) |
Other identities include
 | |  | (21) |
 | |  | (22) |
 | |  | (23) |
 | |  | (24) |
These formulas allow calculations for large
to be decomposed into a chain in which only four quantities must be kept track ofat a time, and the number of steps needed is 
. The chain is particularly simple if has many 2s in itsfactorization.The 
s in a Lucas sequence satisfy the Congruence
 | (25) |
 | (26) |
 | (27) |
References
Dickson, L. E. ``Recurring Series; Lucas' Ribenboim, P. The Little Book of Big Primes. New York: Springer-Verlag, pp. 35-53, 1991.
, 
.'' Ch. 17 in History of the Theory of Numbers, Vol. 1: Divisibility and Primality. New York: Chelsea, pp. 393-411, 1952.
- Scalene Triangle
- Scaling
- Scattering Operator
- Scattering Theory
- Schaar's Identity
- Schanuel's Conjecture
- Schauder Fixed Point Theorem
- Scheme
- Schensted Correspondence
- Scherk's Minimal Surfaces
- Schiffler Point
- Schinzel Circle
- Schinzel's Hypothesis
- Schinzel's Theorem
- Schisma
- Schlegel Graph
- Schläfli Double Six
- Schläfli Function
- Schläfli Integral
- Schläfli Polynomial
- Schläfli's Formula
- Schläfli's Modular Form
- Schläfli Symbol
- Schlömilch's Function
- Schlömilch's Series