| 释义 |
Machin-Like FormulasMachin-like formulas have the form
 | (1) |
 , ,  , and , and 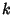 are Positive Integers and are Positive Integers and  and and 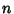 are NonnegativeIntegers. Some such Formulas can be found by converting the Inverse Tangentdecompositions for which are NonnegativeIntegers. Some such Formulas can be found by converting the Inverse Tangentdecompositions for which  in the table of Todd (1949) to Inverse Cotangents. However,this gives only Machin-like formulas in which the smallest term is in the table of Todd (1949) to Inverse Cotangents. However,this gives only Machin-like formulas in which the smallest term is  . .
Maclaurin-like formulas can be derived by writing
 | (2) |
 and and 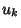 such that such that
 | (3) |
 | (4) |
 | (5) |
 | (6) |
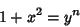 | (7) |
 , 5, .... , 5, ....
There are only four such Formulas,
known as Machin's Formula, Euler's Machin-Like Formula, Hermann's Formula, and Hutton'sFormula. These follow from the identities
Machin-like formulas with two terms can also be generated which do not have integral arc cotangent arguments such asEuler's 
 | (16) |
 | (17) |
Three-term Machin-like formulas include Gauss's Machin-Like Formula
 | (18) |
 | (19) |
The first is due to Stérmer, the second due to Rutherford, and the third due to Dase.
Using trigonometric identities such as
 | (25) |
The efficiency of a Formula is the time it takes to calculate  with the Power series for arctangent with the Power series for arctangent
 | (26) |
 | (27) |
 ,so lower ,so lower  -values correspondto better sums. The best currently known efficiency is 1.51244, which is achieved by the 6-term series -values correspondto better sums. The best currently known efficiency is 1.51244, which is achieved by the 6-term series | | 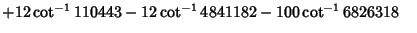 | (28) |
discovered by C.-L. Hwang (1997). Hwang (1997) also discovered the remarkable identitieswhere  , , 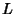 , , 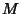 , , 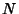 , and , and  are Positive Integers, and are Positive Integers, and
 | (30) |
The following table gives the number  of Machin-like formulas of of Machin-like formulas of 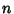 terms in the compilation by Wetherfield andHwang. Except for previously known identities (which are included), the criteria for inclusion are the following: terms in the compilation by Wetherfield andHwang. Except for previously known identities (which are included), the criteria for inclusion are the following: - 1. first term
 digits: measure digits: measure  . . - 2. first term = 8 digits: measure
 . . - 3. first term = 9 digits: measure
 . . - 4. first term =10 digits: measure
 . .
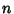 |  |  | | 1 | 1 | 0 | | 2 | 4 | 1.85113 | | 3 | 106 | 1.78661 | | 4 | 39 | 1.58604 | | 5 | 90 | 1.63485 | | 6 | 120 | 1.51244 | | 7 | 113 | 1.54408 | | 8 | 18 | 1.65089 | | 9 | 4 | 1.72801 | | 10 | 78 | 1.63086 | | 11 | 34 | 1.6305 | | 12 | 188 | 1.67458 | | 13 | 37 | 1.71934 | | 14 | 5 | 1.75161 | | 15 | 24 | 1.77957 | | 16 | 51 | 1.81522 | | 17 | 5 | 1.90938 | | 18 | 570 | 1.87698 | | 19 | 1 | 1.94899 | | 20 | 11 | 1.95716 | | 21 | 1 | 1.98938 | | Total | 1500 | 1.51244 |
References
Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, pp. 347-359, 1987.Borwein, J. M. and Borwein, P. B. Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity. New York: Wiley, 1987. Castellanos, D. ``The Ubiquitous Pi. Part I.'' Math. Mag. 61, 67-98, 1988. Conway, J. H. and Guy, R. K. The Book of Numbers. New York: Springer-Verlag, pp. 241-248, 1996. Hwang, C.-L. ``More Machin-Type Identities.'' Math. Gaz., 120-121, March 1997. Lehmer, D. H. ``On Arccotangent Relations for  .'' Amer. Math. Monthly 45, 657-664, 1938. .'' Amer. Math. Monthly 45, 657-664, 1938. Lewin, L. Polylogarithms and Associated Functions. New York: North-Holland, 1981. Lewin, L. Structural Properties of Polylogarithms. Providence, RI: Amer. Math. Soc., 1991. Nielsen, N. Der Euler'sche Dilogarithms. Leipzig, Germany: Halle, 1909. Stérmer, C. ``Sur l'Application de la Théorie des Nombres Entiers Complexes à la Solution en Nombres Rationels  , , 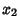 , ..., , ..., 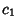 , ,  , ..., , ..., 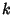 de l'Equation....'' Archiv for Mathematik og Naturvidenskab B 19, 75-85, 1896. de l'Equation....'' Archiv for Mathematik og Naturvidenskab B 19, 75-85, 1896. Todd, J. ``A Problem on Arc Tangent Relations.'' Amer. Math. Monthly 56, 517-528, 1949.  Weisstein, E. W. ``Machin-Like Formulas.'' Mathematica notebook MachinFormulas.m. Weisstein, E. W. ``Machin-Like Formulas.'' Mathematica notebook MachinFormulas.m.
Wetherfield, M. ``The Enhancement of Machin's Formula by Todd's Process.'' Math. Gaz. 80, 333-344, 1996. Wetherfield, M. ``Machin Revisited.'' Math. Gaz., 121-123, March 1997.
|





![]()
![]() with the Power series for arctangent
with the Power series for arctangent![]() of Machin-like formulas of
of Machin-like formulas of ![]() terms in the compilation by Wetherfield andHwang. Except for previously known identities (which are included), the criteria for inclusion are the following:
terms in the compilation by Wetherfield andHwang. Except for previously known identities (which are included), the criteria for inclusion are the following: digits: measure
digits: measure  .
. .
. .
. .
.![]() .'' Amer. Math. Monthly 45, 657-664, 1938.
.'' Amer. Math. Monthly 45, 657-664, 1938.![]() ,
, ![]() , ...,
, ..., ![]() ,
, ![]() , ...,
, ..., ![]() de l'Equation....'' Archiv for Mathematik og Naturvidenskab B 19, 75-85, 1896.
de l'Equation....'' Archiv for Mathematik og Naturvidenskab B 19, 75-85, 1896.![]() Weisstein, E. W. ``Machin-Like Formulas.'' Mathematica notebook MachinFormulas.m.
Weisstein, E. W. ``Machin-Like Formulas.'' Mathematica notebook MachinFormulas.m.