Matrix Norm
Given a Square Matrix ![]() with Complex (or Real) entries, aMatrix Norm
with Complex (or Real) entries, aMatrix Norm ![]() is a Nonnegative number associated with
is a Nonnegative number associated with ![]() having the properties
having the properties
- 1.
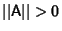 when
when 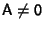 and
and 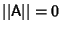 Iff
Iff  ,
, - 2.
 for any Scalar
for any Scalar 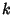 ,
, - 3.
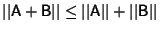 ,
, - 4.
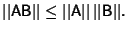
Let
The Maximum Absolute Column Sum Norm ![]() , Spectral Norm
, Spectral Norm ![]() , and Maximum Absolute Row Sum Norm
, and Maximum Absolute Row Sum Norm ![]() satisfy
satisfy
For a Square Matrix, the Spectral Norm, which is the Square Root of the maximum Eigenvalue of
References
Gradshteyn, I. S. and Ryzhik, I. M. Tables of Integrals, Series, and Products, 5th ed. San Diego, CA: Academic Press, pp. 1114-1125, 1979.
- Stationary Value
- Statistic
- Statistical Test
- Statistics
- Staudt-Clausen Theorem
- Steenrod Algebra
- Steenrod-Eilenberg Axioms
- Steenrod's Realization Problem
- Steepest Descent Method
- Steffensen's Inequality
- Steffenson's Formula
- Steinbach Screw
- Steiner Chain
- Steiner Construction
- Steinerian Curve
- Steiner-Lehmus Theorem
- Steiner Points
- Steiner Quadruple System
- Steiner's Ellipse
- Steiner Set
- Steiner's Hypocycloid
- Steiner's Porism
- Steiner's Problem
- Steiner's Segment Problem
- Steiner's Theorem