A farmer wishes to build a rectangular pen with
400 ft of fencing. What shape rectangle gives
the largest area for this given length of fence?
The answer is a 100 ×100 square pen. Any other rect-
angle will have one side shorter than 100 ft, say 100 –
xft, a longer width, 100 + xft, and consequently area
of (100 – x)(100 + x) = 10,000 – x2ft2, which is less
than the area of the square pen.
A square is one of the three regular
POLYGON
s that
provides a
TESSELLATION
of the plane. Two squares of
different sizes also tile the plane. Such a tessellation
holds within it a purely visual proof of P
YTHAGORAS
’
S
THEOREM
.
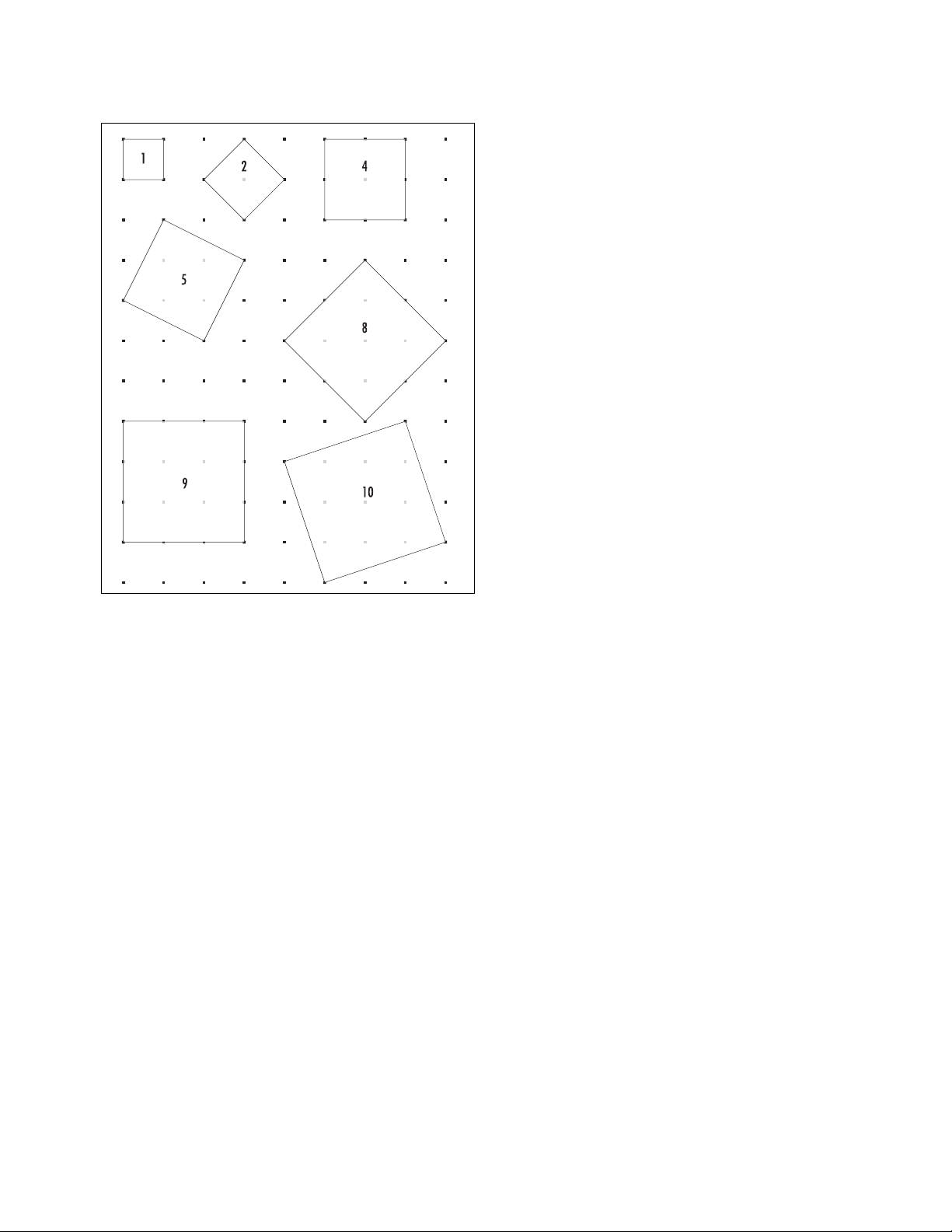
Using a sheet of graph paper, one can draw squares
of areas 1, 2, 4, 5, 8, 9, and 10 units, all with vertices
on the lattice points of the paper, but not squares of
areas 3, 6, or 7 units.
Pythagoras’s theorem shows that one can draw a
square of area Nif, and only if, Nis of the form N= a2
+ b2for some integers aand b. For example, 9 = 32+
02and 5 = 22+ 12. (The side-length of a square of area
5 spans 2 units across and 1 unit over.) Surprisingly,
this set of numbers satisfies the
CLOSURE PROPERTY
under multiplication.
See also
FIGURATE NUMBERS
;
THEOREM
.
square numbers See
FIGURATE NUMBERS
.
square root A number x, that, when multiplied by
itself, produces a given number ais called the square
root of the number a. If x2= a, then we write x= √
–
a.
For example, 3 is a square root of 9, since 3 ×3 = 9,
and zero is a square root of zero, since 0 ×0 = 0. Geo-
metrically, the square root of a positive quantity ais
the side-length of a square whose area is a.
The invention the symbol √
–
, called a radical sign,
for the extraction of square roots is attributed to Ger-
man mathematician Christoff Rudolff (1499–1545).
The name of the symbol comes from the Latin word
radix for “root.” Any quantity that appears under a
radical sign is called a radicand. For example, in the
equation √
–
169 = 13, 169 is the radicand and 13 is the
square root.
Any equation of the form x2= awith a≠0 has two
distinct solutions. Thus every number different from
zero has two distinct square roots. For instance, 3 and
–3 are both square roots of 9. By convention, if ais a
positive quantity, then √
–
ais used to denote the positive
root and –√
–
athe negative square root. For instance, we
write √
–
9 = 3 even though –3 is also a valid square root
of 9.
A study of
EXPONENT
s shows that it is appropriate
to define a number raised to the half power to mean the
square root of that number. Whether that root is positive
or negative is left undefined. Thus, for instance, 9 = ±3.
Attempts to define the square roots of negative
numbers leads to the invention of the
COMPLEX NUM
-
BERS
. In the realm of complex numbers, every number
(except zero) has exactly two square roots.
The square root of any
CONSTRUCTIBLE
number is
again constructible. Thus, given a line segment of
length adrawn on a page, it is possible to construct
from it a second line segment of length √
–
ausing only
the simple tools of a straightedge and a compass.
Greek mathematician T
HEODORUS OF
C
YRENE
(ca.
425
B
.
C
.
E
.) used simple geometric arguments to prove
1
–
2
square root 475
Squares on a lattice