polynomial
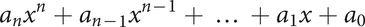
is a polynomial in x with coefficients a0, a1,…, an. When a0, a1,…, an are not all zero, it can be assumed that an ≠ 0 and the polynomial has degree n. For example, 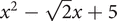 and
and  are polynomials of degrees 2 and 4 respectively. A polynomial can be denoted by f(x) (so that f is a function), and then f(−1), for example, denotes the value of the polynomial when x is replaced by −1. In the same way, it is possible to consider polynomials in x with coefficients from the complex numbers, such as z2 + 2(1−i)z + (15 + 6i), or more generally from other fields and rings. See Fundamental Theorem of Algebra, polynomial ring.
are polynomials of degrees 2 and 4 respectively. A polynomial can be denoted by f(x) (so that f is a function), and then f(−1), for example, denotes the value of the polynomial when x is replaced by −1. In the same way, it is possible to consider polynomials in x with coefficients from the complex numbers, such as z2 + 2(1−i)z + (15 + 6i), or more generally from other fields and rings. See Fundamental Theorem of Algebra, polynomial ring.
- expected monetary value
- expected utility
- expected value
- experiment
- experimental design
- explanatory variable
- explementary angles
- explicit function
- exploratory data analysis
- exponent
- exponential decay
- exponential distribution
- exponential function
- exponential function to base a
- exponential growth
- exponential of a matrix
- exponential series
- exponentiate
- express
- extended complex plane
- extended mean value theorem
- extended metric
- extended real numbers
- extension
- exterior