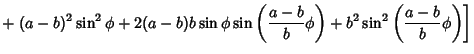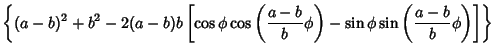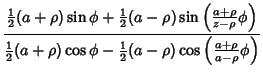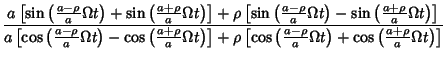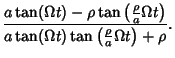| 释义 |
HypocycloidThe curve produced by a small Circle of Radius  rolling around the inside of a large Circle ofRadius rolling around the inside of a large Circle ofRadius 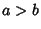 . A hypocycloid is a Hypotrochoid with . A hypocycloid is a Hypotrochoid with  . To derive the equations of the hypocycloid, call theAngle by which a point on the small Circle rotates about its center . To derive the equations of the hypocycloid, call theAngle by which a point on the small Circle rotates about its center  , and the Angle from thecenter of the large Circle to that of the small Circle , and the Angle from thecenter of the large Circle to that of the small Circle 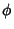 . Then . Then
 | (1) |
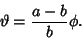 | (2) |
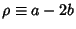 . If . If  , then the first point is at minimum radius, and the Cartesian parametric equations of the hypocycloid are , then the first point is at minimum radius, and the Cartesian parametric equations of the hypocycloid are
If  instead so the first point is at maximum radius (on the Circle), then the equations of the hypocycloid are instead so the first point is at maximum radius (on the Circle), then the equations of the hypocycloid are
An  -cusped non-self-intersecting hypocycloid has -cusped non-self-intersecting hypocycloid has 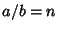 . A 2-cusped hypocycloid is a Line Segment, as can be seenby setting . A 2-cusped hypocycloid is a Line Segment, as can be seenby setting  in equations (3) and (4) and noting that the equations simplify to in equations (3) and (4) and noting that the equations simplify to
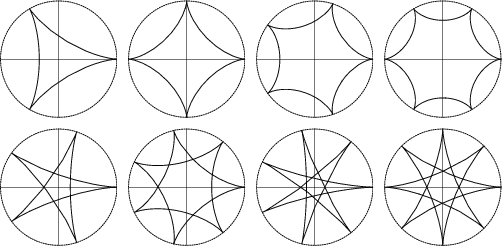
A 3-cusped hypocycloid is called a Deltoid or Tricuspoid, and a 4-cusped hypocycloid is called anAstroid. If  is rational, the curve closes on itself and has is rational, the curve closes on itself and has  cusps. If cusps. If  is Irrational, the curve never closes and fills the entire interior of the Circle. is Irrational, the curve never closes and fills the entire interior of the Circle. -hypocycloids can also be constructed by beginning with the Diameter of a Circle, offsetting one end by aseries of steps while at the same time offsetting the other end by steps -hypocycloids can also be constructed by beginning with the Diameter of a Circle, offsetting one end by aseries of steps while at the same time offsetting the other end by steps  times as large in the opposite direction andextending beyond the edge of the Circle. After traveling around the Circle once, an times as large in the opposite direction andextending beyond the edge of the Circle. After traveling around the Circle once, an  -cusped hypocycloid isproduced, as illustrated above (Madachy 1979). -cusped hypocycloid isproduced, as illustrated above (Madachy 1979).
Let  be the radial distance from a fixed point. For Radius of Torsion be the radial distance from a fixed point. For Radius of Torsion  and Arc Length and Arc Length  , a hypocycloidcan given by the equation , a hypocycloidcan given by the equation
 | (9) |
 | (10) |
 | (11) |
 is the Angle between the Radius Vector and the Tangent to the curve. is the Angle between the Radius Vector and the Tangent to the curve.
The Arc Length of the hypocycloid can be computed as follows
so
for  . Integrating, . Integrating,
The length of a single cusp is then
 | (17) |
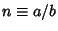 is rational, then the curve closes on itself without intersecting after is rational, then the curve closes on itself without intersecting after  cusps. For cusps. For 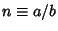 and with and with  , the equations of the hypocycloid become , the equations of the hypocycloid become
and
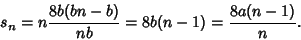 | (20) |
Compute
The Area of one cusp is then
If  is rational, then after is rational, then after  cusps, cusps,
The equation of the hypocycloid can be put in a form which is useful in the solution of Calculus ofVariations problems with radial symmetry. Consider the case  , then , then
But  , so , so  , which gives , which gives
Now let
 | (27) |
 | (28) |
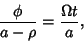 | (29) |
The Polar Angle is
 | (31) |
so
Computing
then gives
 | (37) |
This form is useful in the solution of the Sphere with Tunnel problem, which is the generalization of theBrachistochrone Problem, to find the shape of a tunnel drilled through a Sphere (withgravity  varying according to Gauss's law for gravitation varying according to Gauss's law for gravitation  ) such that the travel time between two points on the surface of the gravity ) such that the travel time between two points on the surface of the gravity  is minimized.See also Cycloid, Epicycloid is minimized.See also Cycloid, Epicycloid
References
Bogomolny, A. ``Cycloids.'' http://www.cut-the-knot.com/pythagoras/cycloids.html.Kreyszig, E. Differential Geometry. New York: Dover, 1991. Lawrence, J. D. A Catalog of Special Plane Curves. New York: Dover, pp. 171-173, 1972. Lee, X. ``Epicycloid and Hypocycloid.''http://www.best.com/~xah/SpecialPlaneCurves_dir/EpiHypocycloid_dir/epiHypocycloid.html. MacTutor History of Mathematics Archive. ``Hypocycloid.''http://www-groups.dcs.st-and.ac.uk/~history/Curves/Hypocycloid.html. Madachy, J. S. Madachy's Mathematical Recreations. New York: Dover, pp. 225-231, 1979. Wagon, S. Mathematica in Action. New York: W. H. Freeman, pp. 50-52, 1991. Yates, R. C. ``Epi- and Hypo-Cycloids.'' A Handbook on Curves and Their Properties. Ann Arbor, MI: J. W. Edwards, pp. 81-85, 1952. |
![]() rolling around the inside of a large Circle ofRadius
rolling around the inside of a large Circle ofRadius ![]() . A hypocycloid is a Hypotrochoid with
. A hypocycloid is a Hypotrochoid with ![]() . To derive the equations of the hypocycloid, call theAngle by which a point on the small Circle rotates about its center
. To derive the equations of the hypocycloid, call theAngle by which a point on the small Circle rotates about its center ![]() , and the Angle from thecenter of the large Circle to that of the small Circle
, and the Angle from thecenter of the large Circle to that of the small Circle ![]() . Then
. Then
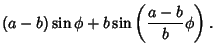
![]() instead so the first point is at maximum radius (on the Circle), then the equations of the hypocycloid are
instead so the first point is at maximum radius (on the Circle), then the equations of the hypocycloid are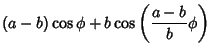

![]() -cusped non-self-intersecting hypocycloid has
-cusped non-self-intersecting hypocycloid has ![]() . A 2-cusped hypocycloid is a Line Segment, as can be seenby setting
. A 2-cusped hypocycloid is a Line Segment, as can be seenby setting ![]() in equations (3) and (4) and noting that the equations simplify to
in equations (3) and (4) and noting that the equations simplify to
![]() -hypocycloids can also be constructed by beginning with the Diameter of a Circle, offsetting one end by aseries of steps while at the same time offsetting the other end by steps
-hypocycloids can also be constructed by beginning with the Diameter of a Circle, offsetting one end by aseries of steps while at the same time offsetting the other end by steps ![]() times as large in the opposite direction andextending beyond the edge of the Circle. After traveling around the Circle once, an
times as large in the opposite direction andextending beyond the edge of the Circle. After traveling around the Circle once, an ![]() -cusped hypocycloid isproduced, as illustrated above (Madachy 1979).
-cusped hypocycloid isproduced, as illustrated above (Madachy 1979).![]() be the radial distance from a fixed point. For Radius of Torsion
be the radial distance from a fixed point. For Radius of Torsion ![]() and Arc Length
and Arc Length ![]() , a hypocycloidcan given by the equation
, a hypocycloidcan given by the equation
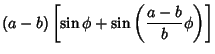

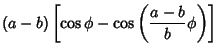






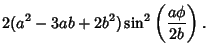
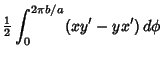
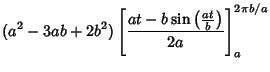

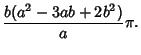

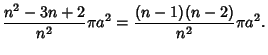
![]() , then
, then