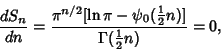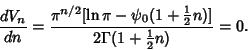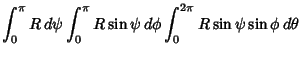| 释义 |
HypersphereThe  -hypersphere (often simply called the -hypersphere (often simply called the  -sphere) is a generalization of the Circle ( -sphere) is a generalization of the Circle ( ) andSphere ( ) andSphere (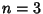 ) to dimensions ) to dimensions  . It is therefore defined as the set of . It is therefore defined as the set of  -tuples of points( -tuples of points(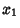 , , 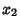 , ..., , ..., 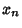 ) such that ) such that
 | (1) |
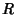 is the Radius of the hypersphere. The Content (i.e., is the Radius of the hypersphere. The Content (i.e.,  -D Volume) of an -D Volume) of an  -hypersphere ofRadius -hypersphere ofRadius 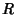 is given by is given by
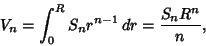 | (2) |
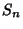 is the hyper-Surface Area of an is the hyper-Surface Area of an  -sphere of unit radius. But, for a unit hypersphere, it must be true that -sphere of unit radius. But, for a unit hypersphere, it must be true that
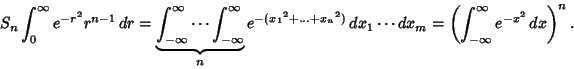 | (3) |
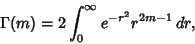 | (4) |
 | (5) |
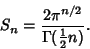 | (6) |
 | (7) |
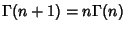 then gives then gives
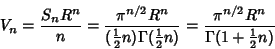 | (8) |
Strangely enough, the hyper-Surface Area and Content reach Maximaand then decrease towards 0 as  increases. The point of Maximal hyper-Surface Area satisfies increases. The point of Maximal hyper-Surface Area satisfies
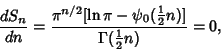 | (9) |
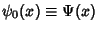 is the Digamma Function. The point of Maximal Content satisfies is the Digamma Function. The point of Maximal Content satisfies
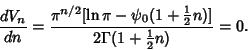 | (10) |
 , but the numerical solutions are , but the numerical solutions are 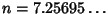 for hyper-Surface Area and for hyper-Surface Area and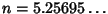 for Content. As a result, the 7-D and 5-D hyperspheres have Maximalhyper-Surface Area and Content, respectively (Le Lionnais 1983). for Content. As a result, the 7-D and 5-D hyperspheres have Maximalhyper-Surface Area and Content, respectively (Le Lionnais 1983).
In 4-D, the generalization of Spherical Coordinates is defined by
The equation for a 4-sphere is
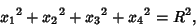 | (15) |
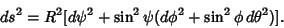 | (16) |
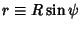 , the Line Element can be rewritten , the Line Element can be rewritten
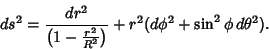 | (17) |
See also Circle, Hypercube, Hypersphere Packing, Mazur's Theorem, Sphere, Tesseract
References
Conway, J. H. and Sloane, N. J. A. Sphere Packings, Lattices, and Groups, 2nd ed. New York: Springer-Verlag, p. 9, 1993.Le Lionnais, F. Les nombres remarquables. Paris: Hermann, p. 58, 1983. Peterson, I. The Mathematical Tourist: Snapshots of Modern Mathematics. New York: W. H. Freeman, pp. 96-101, 1988. |
![]() -hypersphere (often simply called the
-hypersphere (often simply called the ![]() -sphere) is a generalization of the Circle (
-sphere) is a generalization of the Circle (![]() ) andSphere (
) andSphere (![]() ) to dimensions
) to dimensions ![]() . It is therefore defined as the set of
. It is therefore defined as the set of ![]() -tuples of points(
-tuples of points(![]() ,
, ![]() , ...,
, ..., ![]() ) such that
) such that

![]() increases. The point of Maximal hyper-Surface Area satisfies
increases. The point of Maximal hyper-Surface Area satisfies