| 释义 |
Almost IntegerA number which is very close to an Integer. One surprising example involving both e and Pi is
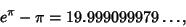 | (1) |
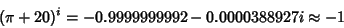 | (2) |
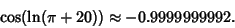 | (3) |
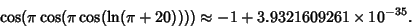 | (4) |
An interesting near-identity is given by
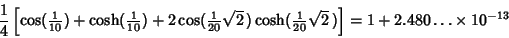 | (5) |
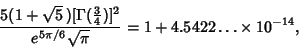 | (6) |
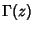 is the Gamma Function (S. Plouffe), and is the Gamma Function (S. Plouffe), and
 | (7) |
A whole class of Irrational ``almost integers'' can be found using the theory ofRamanujan  (1913-14). Such approximations were also studied by Hermite (1913-14). Such approximations were also studied by Hermite  (1859), Kronecker (1859), Kronecker  (1863), and Smith(1965). They can be generated using some amazing (and very deep) properties of the j-Function. Some of thenumbers which are closest approximations to Integers are (1863), and Smith(1965). They can be generated using some amazing (and very deep) properties of the j-Function. Some of thenumbers which are closest approximations to Integers are 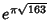 (sometimes known as theRamanujan Constant and which corresponds to the field (sometimes known as theRamanujan Constant and which corresponds to the field  which has Class Number 1 and is theImaginary quadratic field of maximal discriminant), which has Class Number 1 and is theImaginary quadratic field of maximal discriminant), 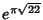 , , 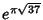 ,and ,and 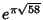 , the last three of which have Ramanujan , the last three of which have Ramanujan  (Berndt1994, Waldschmidt 1988). (Berndt1994, Waldschmidt 1988).
The properties of the j-Function also give rise to the spectacular identity
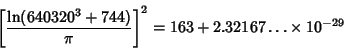 | (8) |
The list below gives numbers of the form 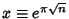 for for  for which for which 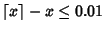 . . Gosper noted that the expression 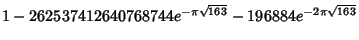 | | 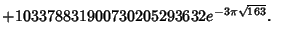 | (9) |
differs from an Integer by a mere 10-59.See also Class Number, j-Function, Pi
References
Berndt, B. C. Ramanujan's Notebooks, Part IV. New York: Springer-Verlag, pp. 90-91, 1994.Hermite, C. ``Sur la théorie des équations modulaires.'' C. R. Acad. Sci. (Paris) 48, 1079-1084 and 1095-1102, 1859. Hermite, C. ``Sur la théorie des équations modulaires.'' C. R. Acad. Sci. (Paris) 49, 16-24, 110-118, and 141-144, 1859. Kronecker, L. ``Über die Klassenzahl der aus Werzeln der Einheit gebildeten komplexen Zahlen.'' Monatsber. K. Preuss. Akad. Wiss. Berlin, 340-345. 1863. Le Lionnais, F. Les nombres remarquables. Paris: Hermann, 1983. Ramanujan, S. ``Modular Equations and Approximations to 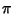 .'' Quart. J. Pure Appl. Math. 45, 350-372, 1913-1914. .'' Quart. J. Pure Appl. Math. 45, 350-372, 1913-1914. Smith, H. J. S. Report on the Theory of Numbers. New York: Chelsea, 1965. Waldschmidt, M. ``Some Transcendental Aspects of Ramanujan's Work.'' In Ramanujan Revisited: Proceedings of the Centenary Conference (Ed. G. E. Andrews, B. C. Berndt, and R. A. Rankin). New York: Academic Press, pp. 57-76, 1988. |
![]() (1913-14). Such approximations were also studied by Hermite
(1913-14). Such approximations were also studied by Hermite ![]() (1859), Kronecker
(1859), Kronecker ![]() (1863), and Smith(1965). They can be generated using some amazing (and very deep) properties of the j-Function. Some of thenumbers which are closest approximations to Integers are
(1863), and Smith(1965). They can be generated using some amazing (and very deep) properties of the j-Function. Some of thenumbers which are closest approximations to Integers are ![]() (sometimes known as theRamanujan Constant and which corresponds to the field
(sometimes known as theRamanujan Constant and which corresponds to the field ![]() which has Class Number 1 and is theImaginary quadratic field of maximal discriminant),
which has Class Number 1 and is theImaginary quadratic field of maximal discriminant), ![]() ,
, ![]() ,and
,and ![]() , the last three of which have Ramanujan
, the last three of which have Ramanujan ![]() (Berndt1994, Waldschmidt 1988).
(Berndt1994, Waldschmidt 1988).![]() for
for ![]() for which
for which ![]() .
.![]() .'' Quart. J. Pure Appl. Math. 45, 350-372, 1913-1914.
.'' Quart. J. Pure Appl. Math. 45, 350-372, 1913-1914.