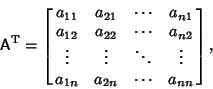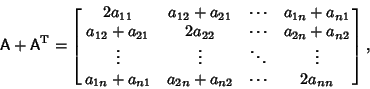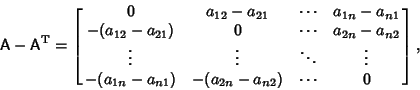| 释义 |
Antisymmetric MatrixAn antisymmetric matrix is a Matrix which satisfies the identity
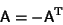 | (1) |
 is the Matrix Transpose. In component notation, this becomes is the Matrix Transpose. In component notation, this becomes
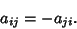 | (2) |
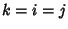 , the requirement becomes , the requirement becomes
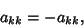 | (3) |
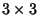 antisymmetric matrix is of the form antisymmetric matrix is of the form
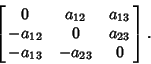 | (4) |
Applying 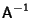 to both sides of the antisymmetrycondition gives to both sides of the antisymmetrycondition gives
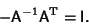 | (5) |
 | (6) |
 | (7) |
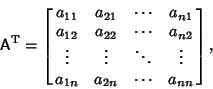 | (8) |
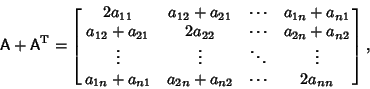 | (9) |
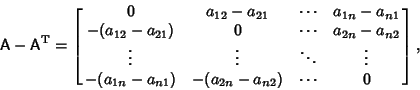 | (10) |
|
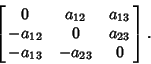
![]() to both sides of the antisymmetrycondition gives
to both sides of the antisymmetrycondition gives