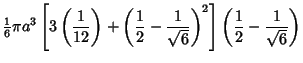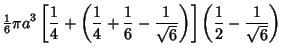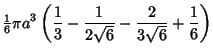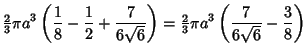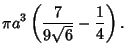| 释义 |
Square PyramidA square pyramid is a Pyramid with a Square base. If the top of the pyramid is cut off by a Plane, asquare Pyramidal Frustum is obtained. If the four Triangles of the square pyramid areEquilateral, the square pyramid is the ``regular'' Polyhedron known as JohnsonSolid 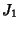 and, for side length and, for side length  , has height , has height
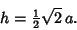 | (1) |
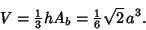 | (2) |
 | (3) |
 is the height and is the height and  is the length of a side of the base. is the length of a side of the base.
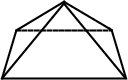
Consider a Hemisphere placed on the base of a square pyramid (having side lengths  and height and height  ). Further, let thehemisphere be tangent to the four apex edges. Then what is the volume of the Hemisphere which is interior thepyramid (Cipra 1993)? ). Further, let thehemisphere be tangent to the four apex edges. Then what is the volume of the Hemisphere which is interior thepyramid (Cipra 1993)?
From Fig. (a), the Circumradius of the base is  . Now find . Now find  in terms of in terms of  and and  . Fig. (b) shows aCross-Section cut by the plane through the pyramid's apex, one of the base's vertices, and the base center. This figuregives . Fig. (b) shows aCross-Section cut by the plane through the pyramid's apex, one of the base's vertices, and the base center. This figuregives
so the Slant Height is
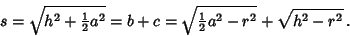 | (6) |
 gives gives
 | (7) |
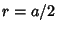 , and , and
 | (8) |
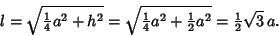 | (9) |
 and and  . .
 | (10) |
 and and  , and , and  is given by is given by
 | (11) |
 | (12) |
 | (13) |
 | (14) |
 | (15) |
so
Therefore, the volume within the pyramid is
This problem appeared in the Japanese scholastic aptitude test (Cipra 1993).See also Square Pyramidal Number
References
Cipra, B. ``An Awesome Look at Japan Math SAT.'' Science 259, 22, 1993.
|

![]() and, for side length
and, for side length ![]() , has height
, has height
![]() and height
and height ![]() ). Further, let thehemisphere be tangent to the four apex edges. Then what is the volume of the Hemisphere which is interior thepyramid (Cipra 1993)?
). Further, let thehemisphere be tangent to the four apex edges. Then what is the volume of the Hemisphere which is interior thepyramid (Cipra 1993)?![]() . Now find
. Now find ![]() in terms of
in terms of ![]() and
and ![]() . Fig. (b) shows aCross-Section cut by the plane through the pyramid's apex, one of the base's vertices, and the base center. This figuregives
. Fig. (b) shows aCross-Section cut by the plane through the pyramid's apex, one of the base's vertices, and the base center. This figuregives