| 释义 |
Greedy AlgorithmAn algorithm used to recursively construct a Set of objects from the smallest possible constituent parts.
Given a Set of  Integers ( Integers ( , ,  , ..., , ...,  ) with ) with 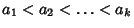 , a greedyalgorithm can be used to find a Vector of coefficients ( , a greedyalgorithm can be used to find a Vector of coefficients (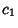 , ,  , ..., , ..., 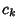 ) such that ) such that
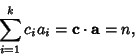 | (1) |
 is the Dot Product, for some given Integer is the Dot Product, for some given Integer  . This can be accomplished by letting . This can be accomplished by letting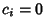 for for  , ..., , ...,  and setting and setting
 | (2) |
 as as
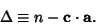 | (3) |
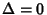 at any step, a representation has been found. Otherwise, decrement the Nonzero at any step, a representation has been found. Otherwise, decrement the Nonzero 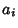 term with least term with least , set all , set all  for for  , and build up the remaining terms from , and build up the remaining terms from
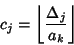 | (4) |
 , ..., 1 until , ..., 1 until 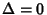 or all possibilities have been exhausted. or all possibilities have been exhausted.
For example, McNugget Numbers are numbers which are representable using only 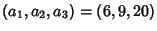 . Taking . Taking  and applying the algorithm iteratively gives the sequence (0, 0, 3), (0, 2, 2), (2, 1, 2), (3,0, 2), (1, 4, 1), at which point and applying the algorithm iteratively gives the sequence (0, 0, 3), (0, 2, 2), (2, 1, 2), (3,0, 2), (1, 4, 1), at which point 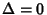 . 62 is therefore a McNugget Number with . 62 is therefore a McNugget Number with
 | (5) |
If any Integer  can be represented with can be represented with 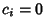 or 1 using a sequence ( or 1 using a sequence ( , ,  , ...), then this sequenceis called a Complete Sequence. , ...), then this sequenceis called a Complete Sequence.
A greedy algorithm can also be used to break down arbitrary fractions into Unit Fractions in a finite numberof steps. For a Fraction  , find the least Integer , find the least Integer 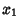 such that such that  , i.e., , i.e.,
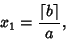 | (6) |
 is the Ceiling Function. Then find the least Integer is the Ceiling Function. Then find the least Integer  such that such that  .Iterate until there is no remainder. The Algorithm gives two or fewer terms for .Iterate until there is no remainder. The Algorithm gives two or fewer terms for  and and  , three or fewer termsfor , three or fewer termsfor 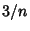 , and four or fewer for , and four or fewer for 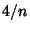 . .
Paul Erdös and E. G. Strays have conjectured that the Diophantine Equation
 | (7) |
 | (8) |
|
![]() Integers (
Integers (![]() ,
, ![]() , ...,
, ..., ![]() ) with
) with ![]() , a greedyalgorithm can be used to find a Vector of coefficients (
, a greedyalgorithm can be used to find a Vector of coefficients (![]() ,
, ![]() , ...,
, ..., ![]() ) such that
) such that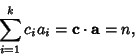
![]() . Taking
. Taking ![]() and applying the algorithm iteratively gives the sequence (0, 0, 3), (0, 2, 2), (2, 1, 2), (3,0, 2), (1, 4, 1), at which point
and applying the algorithm iteratively gives the sequence (0, 0, 3), (0, 2, 2), (2, 1, 2), (3,0, 2), (1, 4, 1), at which point ![]() . 62 is therefore a McNugget Number with
. 62 is therefore a McNugget Number with![]() can be represented with
can be represented with ![]() or 1 using a sequence (
or 1 using a sequence (![]() ,
, ![]() , ...), then this sequenceis called a Complete Sequence.
, ...), then this sequenceis called a Complete Sequence.![]() , find the least Integer
, find the least Integer ![]() such that
such that ![]() , i.e.,
, i.e.,