“Confluent Hypergeometric Function of the First Kind”的概念、定义、习题解题方法及翻译-数学辞典

单词

Confluent Hypergeometric Function of the First Kind

释义

Confluent Hypergeometric Function of the First Kind

The confluent hypergeometric function is a degenerate form the Hypergeometric Function which arisesas a solution the Confluent Hypergeometric Differential Equation. It is commonly denoted ,, or , and is also known as Kummer's Function of the first kind. An alternate form of thesolution to the Confluent Hypergeometric Differential Equation is known as the Whittaker Function.

The confluent hypergeometric function has a Hypergeometric Series given by

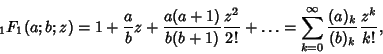(1)

where

and

are Pochhammer Symbols. If

and

areIntegers,

, and either

, then the series yields a Polynomial with a finitenumber of terms. If

is an Integer

, then

is undefined. The confluent hypergeometricfunction also has an integral representation

(2)

(Abramowitz and Stegun 1972, p. 505).

Bessel Functions, the Error Function, the incomplete Gamma Function, HermitePolynomial, Laguerre Polynomial, as well as other are all special cases of this function (Abramowitz and Stegun1972, p. 509).

Kummer's Second Formula gives


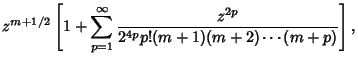			(3)

where

is the Confluent Hypergeometric Function and

, ....

See also Confluent Hypergeometric Differential Equation, Confluent Hypergeometric Function of the Second Kind,Confluent Hypergeometric Limit Function, Generalized Hypergeometric Function, Heine HypergeometricSeries, Hypergeometric Function, Hypergeometric Series, Kummer's Formulas, Weber-Sonine Formula,Whittaker Function

References

Abramowitz, M. and Stegun, C. A. (Eds.). ``Confluent Hypergeometric Functions.'' Ch. 13 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 503-515, 1972.

Arfken, G. ``Confluent Hypergeometric Functions.'' §13.6 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 753-758, 1985.

Iyanaga, S. and Kawada, Y. (Eds.). ``Hypergeometric Function of Confluent Type.'' Appendix A, Table 19.I in Encyclopedic Dictionary of Mathematics. Cambridge, MA: MIT Press, p. 1469, 1980.

Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 551-554 and 604-605, 1953.

Slater, L. J. Confluent Hypergeometric Functions. Cambridge, England: Cambridge University Press, 1960.

Spanier, J. and Oldham, K. B. ``The Kummer Function .'' Ch. 47 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 459-469, 1987.

随便看

数学辞典收录了8975条数学词条，基本涵盖了常用数学知识及数学英语单词词组的翻译及用法，是数学学习的有利工具。