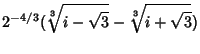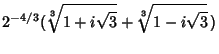| 释义 |
Trigonometry Values Pi/9Trigonometric functions of 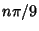 radians for radians for 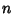 an integer not divisible by 3 (e.g., 40° and 80°) cannotbe expressed in terms of sums, products, and finite root extractions on real rational numbers because 9 is not aproduct of distinct Fermat Primes. This also means that the Nonagon is not aConstructible Polygon. an integer not divisible by 3 (e.g., 40° and 80°) cannotbe expressed in terms of sums, products, and finite root extractions on real rational numbers because 9 is not aproduct of distinct Fermat Primes. This also means that the Nonagon is not aConstructible Polygon.
However, exact expressions involving roots of complex numbers can still be derived using the trigonometric identity
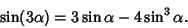 | (1) |
 and and 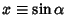 . Then the above identity gives the Cubic Equation . Then the above identity gives the Cubic Equation
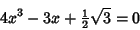 | (2) |
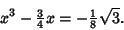 | (3) |
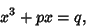 | (4) |
The Discriminant is then
There are therefore three Real distinct roots, which are approximately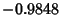 , 0.3240, and 0.6428. We want the one in the first Quadrant, which is 0.3240. , 0.3240, and 0.6428. We want the one in the first Quadrant, which is 0.3240.
Similarly,
Because of the Newton's Relations, we have the identities
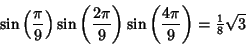 | (10) |
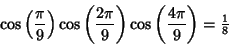 | (11) |
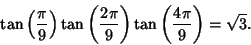 | (12) |
|
![]() radians for
radians for ![]() an integer not divisible by 3 (e.g., 40° and 80°) cannotbe expressed in terms of sums, products, and finite root extractions on real rational numbers because 9 is not aproduct of distinct Fermat Primes. This also means that the Nonagon is not aConstructible Polygon.
an integer not divisible by 3 (e.g., 40° and 80°) cannotbe expressed in terms of sums, products, and finite root extractions on real rational numbers because 9 is not aproduct of distinct Fermat Primes. This also means that the Nonagon is not aConstructible Polygon.