| 释义 |
Matrix InverseA Matrix 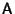 has an inverse Iff the Determinant has an inverse Iff the Determinant 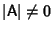 . For a . For a  Matrix Matrix
 | (1) |
 | (2) |
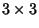 Matrix, Matrix,
 | (3) |
 matrix can be inverted using methods such as the Gauss-Jordan Elimination, GaussianElimination, or LU Decomposition. matrix can be inverted using methods such as the Gauss-Jordan Elimination, GaussianElimination, or LU Decomposition.
The inverse of a Product  of Matrices of Matrices 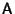 and and  can be expressedin terms of can be expressedin terms of  and and 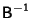 . Let . Let
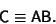 | (4) |
 | (5) |
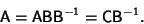 | (6) |
 | (7) |
 | (8) |
 | (9) |
References
Ben-Israel, A. and Greville, T. N. E. Generalized Inverses: Theory and Applications. New York: Wiley, 1977.Nash, J. C. Compact Numerical Methods for Computers: Linear Algebra and Function Minimisation, 2nd ed. Bristol, England: Adam Hilger, pp. 24-26, 1990. Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. ``Is Matrix Inversion an  Process?'' §2.11 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 95-98, 1992. Process?'' §2.11 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 95-98, 1992.
|
![]() has an inverse Iff the Determinant
has an inverse Iff the Determinant ![]() . For a
. For a ![]() Matrix
Matrix
![]() of Matrices
of Matrices ![]() and
and ![]() can be expressedin terms of
can be expressedin terms of ![]() and
and ![]() . Let
. Let![]() Process?'' §2.11 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 95-98, 1992.
Process?'' §2.11 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 95-98, 1992.