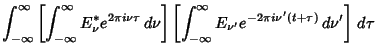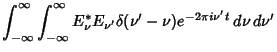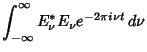| 释义 |
Wiener-Khintchine TheoremRecall the definition of the Autocorrelation function  of a function of a function  , ,
 | (1) |
 is defined by is defined by
 | (2) |
 | (3) |
 and and  into the Autocorrelation function therefore gives into the Autocorrelation function therefore gives
so, amazingly, the Autocorrelation is simply given by the Fourier Transform of the Absolute Squareof 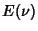 , ,
 | (5) |
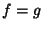 .See also Autocorrelation, Cross-Correlation Theorem, Fourier Transform .See also Autocorrelation, Cross-Correlation Theorem, Fourier Transform
|
![]() of a function
of a function ![]() ,
,