| 释义 |
Parabola EvoluteGiven a Parabola
 | (1) |
 | (2) |
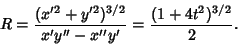 | (3) |
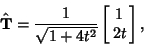 | (4) |
and
 | (9) |
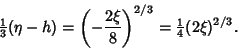 | (10) |
 | (11) |
|