| 释义 |
Elliptic Partial Differential EquationA second-order Partial Differential Equation, i.e., one of the form
 | (1) |
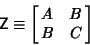 | (2) |
 on on 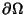 , where , where
 | (3) |
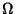 .See also Hyperbolic Partial Differential Equation, Parabolic Partial Differential Equation,Partial Differential Equation .See also Hyperbolic Partial Differential Equation, Parabolic Partial Differential Equation,Partial Differential Equation
|