| 释义 |
Hermitian OperatorA Hermitian Operator  is one which satisfies is one which satisfies
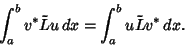 | (1) |
 is Self-Adjoint and satisfiesthe boundary conditions is Self-Adjoint and satisfiesthe boundary conditions
 | (2) |
 is second-order andlinear. In order to prove that Eigenvalues must be Real andEigenfunctions Orthogonal, consider is second-order andlinear. In order to prove that Eigenvalues must be Real andEigenfunctions Orthogonal, consider
 | (3) |
 such that such that
 | (4) |
 | (5) |
 and (5) by and (5) by 
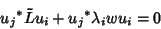 | (6) |
 | (7) |
 | (8) |
 | (9) |
 is Hermitian, the left side vanishes. is Hermitian, the left side vanishes.
 | (10) |
 and and  are not degenerate, then are not degenerate, then  , so theEigenfunctions are Orthogonal. If theEigenvalues are degenerate, the Eigenfunctions are not necessarilyorthogonal. Now take , so theEigenfunctions are Orthogonal. If theEigenvalues are degenerate, the Eigenfunctions are not necessarilyorthogonal. Now take  . .
 | (11) |
 , so we have , so we have 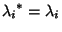 and the Eigenvaluesare real. and the Eigenvaluesare real.
For a Hermitian operator  , ,
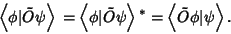 | (12) |
 | (13) |
 and and  , ,
 | (14) |
 with Eigenvalue with Eigenvalue  , ,
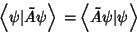 | (15) |
 | (16) |
 or or  . But . But  Iff Iff  , so , so
 | (17) |
 , namely that Hermitian operators produce Real expectation values. Every observable must therefore have a corresponding Hermitian operator. Furthermore, , namely that Hermitian operators produce Real expectation values. Every observable must therefore have a corresponding Hermitian operator. Furthermore,
 | (18) |
 | (19) |
 . Then . Then
 | (20) |
 (i.e., (i.e.,  ), ),
 | (21) |
 (i.e., (i.e.,  ), ),
 | (22) |
 | (23) |
 and and  , ,
 | (24) |
 equals equals 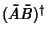 , and is therefore Hermitian, only if , and is therefore Hermitian, only if
 | (25) |
 , ,
so  is Hermitian. is Hermitian.
so  is Hermitian. Similarly, is Hermitian. Similarly,
 | (28) |
 is Hermitian. is Hermitian.
Define the Hermitian conjugate operator  by by
 | (29) |
 . Furthermore, given two Hermitian operators . Furthermore, given two Hermitian operators  and and  , ,
so
 | (31) |
 | (32) |
References
Arfken, G. ``Hermitian (Self-Adjoint) Operators.'' §9.2 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 504-506 and 510-516, 1985. |
![]() is one which satisfies
is one which satisfies![]() ,
,![]() by
by