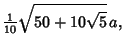| 释义 |
IcosahedronA Platonic Solid ( ) with 12 Vertices, 30 Edges, and 20 equivalentEquilateral Triangle faces ) with 12 Vertices, 30 Edges, and 20 equivalentEquilateral Triangle faces  . It is described by the Schläfli Symbol . It is described by the Schläfli Symbol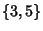 . It is also Uniform Polyhedron . It is also Uniform Polyhedron  and has Wythoff Symbol and has Wythoff Symbol  . The icosahedron hasthe Icosahedral Group . The icosahedron hasthe Icosahedral Group 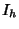 of symmetries. of symmetries.
A plane Perpendicular to a  axis of an icosahedron cuts the solid in a regular Decagonal Cross-Section (Holden 1991, pp. 24-25). axis of an icosahedron cuts the solid in a regular Decagonal Cross-Section (Holden 1991, pp. 24-25).
A construction for an icosahedron with side length  places the end vertices at places the end vertices at 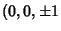 )and the central vertices around two staggered Circles of Radii )and the central vertices around two staggered Circles of Radii  andheights andheights 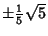 , giving coordinates , giving coordinates
 | (1) |
 , 1, ..., 4, where all the plus signs or minus signs are taken together. Explicitly, these coordinatesare , 1, ..., 4, where all the plus signs or minus signs are taken together. Explicitly, these coordinatesare
By a suitable rotation, the Vertices of an icosahedron of side length 2 can also be placedat  , , 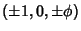 , and , and 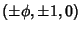 , where , where  is the Golden Ratio. Thesepoints divide the Edges of an Octahedron into segments with lengths in the ratio is the Golden Ratio. Thesepoints divide the Edges of an Octahedron into segments with lengths in the ratio . .
The Dual Polyhedron of the icosahedron is the Dodecahedron. There are 59distinct icosahedra when each Triangle is colored differently (Coxeter 1969).
To derive the Volume of an icosahedron having edge length  , consider the orientation so that twoVertices are oriented on top and bottom. The vertical distance between the top and bottomPentagonal Dipyramids is then given by , consider the orientation so that twoVertices are oriented on top and bottom. The vertical distance between the top and bottomPentagonal Dipyramids is then given by
 | (7) |
 | (8) |
 of the pentagon is of the pentagon is
 | (9) |
 | (10) |
which is identical to the radius of a Pentagon of side  . The Circumradius is then . The Circumradius is then
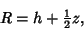 | (12) |
 | (13) |
Taking the square root gives the Circumradius
 | (15) |
 | (16) |
so
 | (18) |
The Area of one face is the Area of an Equilateral Triangle
 | (19) |

Apollonius showed that
 | (21) |
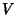 is the volume and is the volume and  the surface area.See also Augmented Tridiminished Icosahedron, Decagon, Dodecahedron, Great Icosahedron,Icosahedron Stellations, Metabidiminished Icosahedron, Tridiminished Icosahedron, Trigonometry Values Pi/5 the surface area.See also Augmented Tridiminished Icosahedron, Decagon, Dodecahedron, Great Icosahedron,Icosahedron Stellations, Metabidiminished Icosahedron, Tridiminished Icosahedron, Trigonometry Values Pi/5
References
Coxeter, H. S. M. Introduction to Geometry, 2nd ed. New York: Wiley, 1969.Davie, T. ``The Icosahedron.'' http://www.dcs.st-and.ac.uk/~ad/mathrecs/polyhedra/icosahedron.html. Holden, A. Shapes, Space, and Symmetry. New York: Dover, 1991. Klein, F. Lectures on the Icosahedron. New York: Dover, 1956. Pappas, T. ``The Icosahedron & the Golden Rectangle.'' The Joy of Mathematics. San Carlos, CA: Wide World Publ./Tetra, p. 115, 1989.
|
![]() ) with 12 Vertices, 30 Edges, and 20 equivalentEquilateral Triangle faces
) with 12 Vertices, 30 Edges, and 20 equivalentEquilateral Triangle faces ![]() . It is described by the Schläfli Symbol
. It is described by the Schläfli Symbol![]() . It is also Uniform Polyhedron
. It is also Uniform Polyhedron ![]() and has Wythoff Symbol
and has Wythoff Symbol ![]() . The icosahedron hasthe Icosahedral Group
. The icosahedron hasthe Icosahedral Group ![]() of symmetries.
of symmetries.![]() axis of an icosahedron cuts the solid in a regular Decagonal Cross-Section (Holden 1991, pp. 24-25).
axis of an icosahedron cuts the solid in a regular Decagonal Cross-Section (Holden 1991, pp. 24-25).![]() places the end vertices at
places the end vertices at ![]() )and the central vertices around two staggered Circles of Radii
)and the central vertices around two staggered Circles of Radii ![]() andheights
andheights ![]() , giving coordinates
, giving coordinates




![]() , consider the orientation so that twoVertices are oriented on top and bottom. The vertical distance between the top and bottomPentagonal Dipyramids is then given by
, consider the orientation so that twoVertices are oriented on top and bottom. The vertical distance between the top and bottomPentagonal Dipyramids is then given by