四、域

[域的定义与例子]  一个具有单位元的交换环R，若至少含有一个非零元，并且每个非零元a恒有逆，则称R为一个域.

例1                       例1         数域F（有理数域Q、实数域R、复数域C等）都是域.

例2                       例2         数域F上的一切有理分式 （且）在有理分式的加法和乘法之下组成一个域，称为数域F上的有理分式域.

[域的基本性质]

1^o域没有零因子.

2^o若集F在两个二元运算（加法和乘法）下满足下列条件，则F为一个域：

(i)  F是以零为单位元的加法群；

(ii) 由除零外的F的一切元组成的集在乘法下是一个交换群；

(iii) 乘法对加法是可分配的，即.

3^o在域F中，方程（，且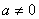）有唯一的解，并可记作.

4^o在域F中，成立指数定律：

式中m，n为任意整数，a，b为F中任意两个元素，只对非零元素才能有负整数的幂.

5^o若把域F的单元e的n倍简记作n，则F中任一元a的n倍就是n与a的积.