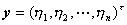§5  二次型与埃尔米特型

一、一、二次型

[双线性型]  若2n个实（或复）变数， 的一个二次齐次多项式

                                                           （1）

称为双线性型，式中

                        ，

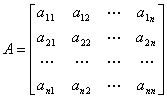
    [二次型]  关于n个实（或复）变数的一个二次齐次多项式

                                              （2）

称为二次型，式中，是矩阵A的对称部分，即的元素是.

表达式（2）恒等于零的充分必要条件是：A是反对称的.

当矩阵A是对称的，则称二次型是对称的. 当矩阵A是实的（是实数），则称二次型是实的. 由（2）可知，每个二次型都可化为对称的.

一个实对称二次型当对每组不全为零的实数，使得，或，则分别称二次型是正定的，负定的，半正定的或半负定的. 其他一切实对称二次型称为不定的（即的符号与有关）或恒等于零.

[化二次型为标准型]

1^o一个线性变换

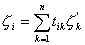
                                                       （3）

或                            

把每个二次型（2）变为关于新变数的一个二次型

                                                       （4）

其中              

或                           

若A是对称的，则也是对称的；若A和T都是实的，则也是实的.

2^o对每个实对称二次型，存在具实系数的线性变换（3），使得在（4）中的矩阵是对角线矩阵，所以

                                                     （5）

在（5）式中系数不等于零的个数r与所采用的对角化的变换无关，并且等于已知矩阵A的秩，r称为二次型的秩. （5）式中系数的正数与负数个数之差也与所采用的对角线化的变换无关（即雅可比-西尔维斯特惯性定律），它称为二次型的符号差.

3^o特别，对每个实对称二次型，存在一个对应于实正交矩阵T的线性变换，可把二次型化为标准型，即

                                                           （6） 

式中实数是已知矩阵A的特征值.

4^o再施行变换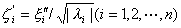，表达式（6）化为

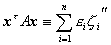
式中等于1，或0，分别对应于特征值是正的，负的或零.

[两个二次型的联立简化]  给定两个实对称二次型，，其中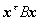是正定的，我们能求出一个实变换（3），它可以把，同时化为标准型. 特别是存在一个实变换（3），使

实数是矩阵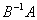的特征值，它们是n次代数方程

的根

    [正定等的判别法] 

    1^o一个实对称二次型是正定，负定，半正定，半负定，不定或恒等于零的充分必要条件是：矩阵的特征值（一定是实的）分别都是正的，都是负的，都是非负的，都是非正的，符号不同或都等于零.

          2^o一个实对称二次型是正定或半正定的充分必要条件是：的每个主子式

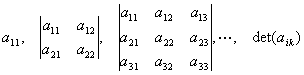
都是正的或非负的.

3^o一个实对称二次型为负定或半负定的充分必要条件是：分别是正定或半正定.

4^o一个实矩阵A是一个半正定矩阵的充分必要条件是：. 若B是非奇异的，则A是正定的.

5^o若A与B都是正定的或负定的，则AB也都是正定的或负定的. 每个正定矩阵A有唯一的决定于（Q是正定的）的一对平方根Q，.