| 释义 |
Gaussian CurvatureAn intrinsic property of a space independent of the coordinate system used to describe it. The Gaussian curvature of aRegular Surface in 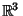 at a point p is formally defined as at a point p is formally defined as
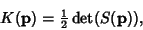 | (1) |
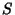 is the Shape Operator and det denotes the Determinant. is the Shape Operator and det denotes the Determinant.
If 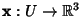 is a Regular Patch, then the Gaussian curvature is given by is a Regular Patch, then the Gaussian curvature is given by
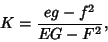 | (2) |
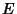 , , 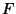 , and , and  are coefficients of the first Fundamental Form and are coefficients of the first Fundamental Form and  , ,  , and , and  are coefficients of the second Fundamental Form (Gray 1993, p. 282). The Gaussian curvaturecan be given entirely in terms of the first Fundamental Form are coefficients of the second Fundamental Form (Gray 1993, p. 282). The Gaussian curvaturecan be given entirely in terms of the first Fundamental Form
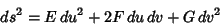 | (3) |
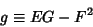 | (4) |
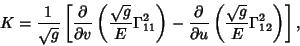 | (5) |
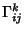 are the Connection Coefficients. Equivalently, are the Connection Coefficients. Equivalently,
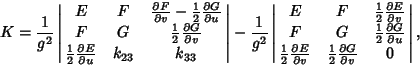 | (6) |
Writing this out,
The Gaussian curvature is also given by
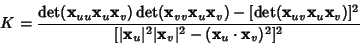 | (10) |
where 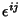 is the Levi-Civita Symbol, is the Levi-Civita Symbol,  is the unit Normal Vector and is the unit Normal Vector and  is theunit Tangent Vector. The Gaussian curvature is also given by is theunit Tangent Vector. The Gaussian curvature is also given by
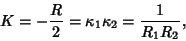 | (12) |
 is the Curvature Scalar, is the Curvature Scalar, 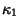 and and 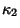 the Principal Curvatures, and the Principal Curvatures, and  and and 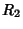 thePrincipal Radii of Curvature. For a Monge Patch with thePrincipal Radii of Curvature. For a Monge Patch with 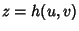 , ,
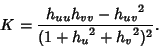 | (13) |
The Gaussian curvature  and Mean Curvature and Mean Curvature 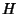 satisfy satisfy
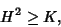 | (14) |
 | (15) |
If p is a point on a Regular Surface  and and 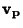 and and 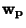 are tangentvectors to are tangentvectors to 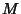 at p, then the Gaussian curvature of at p, then the Gaussian curvature of 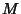 at p is related to the Shape Operator at p is related to the Shape Operator 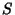 by by
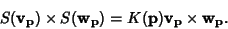 | (16) |
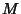 which is everywhere Perpendicular to which is everywhere Perpendicular to 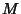 , and let , and let and and 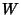 be Vector Fields tangent to be Vector Fields tangent to 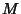 such that such that 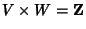 , then , then
 | (17) |
For a Sphere, the Gaussian curvature is 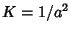 . For Euclidean Space, the Gaussian curvature is . For Euclidean Space, the Gaussian curvature is  . ForGauss-Bolyai-Lobachevsky Space, the Gaussian curvature is . ForGauss-Bolyai-Lobachevsky Space, the Gaussian curvature is 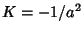 . A Flat Surface is a Regular Surfaceand special class of Minimal Surface on which Gaussian curvature vanishes everywhere. . A Flat Surface is a Regular Surfaceand special class of Minimal Surface on which Gaussian curvature vanishes everywhere.
A point p on a Regular Surface 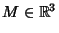 is classified based on the sign of is classified based on the sign of 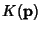 as given in thefollowing table (Gray 1993, p. 280), where as given in thefollowing table (Gray 1993, p. 280), where 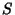 is the Shape Operator. is the Shape Operator. | Sign | Point | 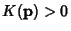 | Elliptic Point | 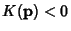 | Hyperbolic Point | 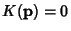 but but 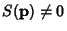 | Parabolic Point | 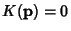 and and  | Planar Point |
A surface on which the Gaussian curvature  is everywhere Positive is called Synclastic, while asurface on which is everywhere Positive is called Synclastic, while asurface on which  is everywhere Negative is called Anticlastic. Surfaces with constant Gaussiancurvature include the Cone, Cylinder, Kuen Surface,Plane, Pseudosphere, and Sphere. Of these, the Coneand Cylinderare the only Flat Surfaces of Revolution. is everywhere Negative is called Anticlastic. Surfaces with constant Gaussiancurvature include the Cone, Cylinder, Kuen Surface,Plane, Pseudosphere, and Sphere. Of these, the Coneand Cylinderare the only Flat Surfaces of Revolution. See also Anticlastic, Brioschi Formula, Developable Surface, Elliptic Point, Flat Surface,Hyperbolic Point, Integral Curvature, Mean Curvature, Metric Tensor, Minimal Surface,Parabolic Point, Planar Point, Synclastic, Umbilic Point
References
Geometry Center. ``Gaussian Curvature.'' http://www.geom.umn.edu/zoo/diffgeom/surfspace/concepts/curvatures/gauss-curv.html.Gray, A. ``The Gaussian and Mean Curvatures'' and ``Surfaces of Constant Gaussian Curvature.'' §14.5 and Ch. 19 in Modern Differential Geometry of Curves and Surfaces. Boca Raton, FL: CRC Press, pp. 279-285 and 375-387, 1993. |
![]() at a point p is formally defined as
at a point p is formally defined as![]() is a Regular Patch, then the Gaussian curvature is given by
is a Regular Patch, then the Gaussian curvature is given by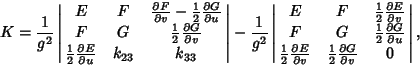
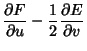
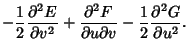
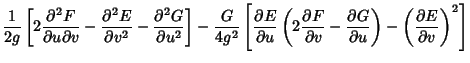
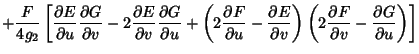
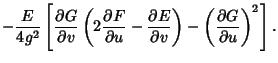
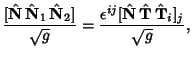
![]() and Mean Curvature
and Mean Curvature ![]() satisfy
satisfy![]() and
and ![]() and
and ![]() are tangentvectors to
are tangentvectors to ![]() at p, then the Gaussian curvature of
at p, then the Gaussian curvature of ![]() at p is related to the Shape Operator
at p is related to the Shape Operator ![]() by
by![]() . For Euclidean Space, the Gaussian curvature is
. For Euclidean Space, the Gaussian curvature is ![]() . ForGauss-Bolyai-Lobachevsky Space, the Gaussian curvature is
. ForGauss-Bolyai-Lobachevsky Space, the Gaussian curvature is ![]() . A Flat Surface is a Regular Surfaceand special class of Minimal Surface on which Gaussian curvature vanishes everywhere.
. A Flat Surface is a Regular Surfaceand special class of Minimal Surface on which Gaussian curvature vanishes everywhere.![]() is classified based on the sign of
is classified based on the sign of ![]() as given in thefollowing table (Gray 1993, p. 280), where
as given in thefollowing table (Gray 1993, p. 280), where ![]() is the Shape Operator.
is the Shape Operator.![]() is everywhere Positive is called Synclastic, while asurface on which
is everywhere Positive is called Synclastic, while asurface on which ![]() is everywhere Negative is called Anticlastic. Surfaces with constant Gaussiancurvature include the Cone, Cylinder, Kuen Surface,Plane, Pseudosphere, and Sphere. Of these, the Coneand Cylinderare the only Flat Surfaces of Revolution.
is everywhere Negative is called Anticlastic. Surfaces with constant Gaussiancurvature include the Cone, Cylinder, Kuen Surface,Plane, Pseudosphere, and Sphere. Of these, the Coneand Cylinderare the only Flat Surfaces of Revolution.