| 释义 |
Cylindrical CoordinatesCylindrical coordinates are a generalization of 2-D Polar Coordinates to 3-D by superposing a height (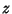 ) axis. Unfortunately, there are a number of different notations used for the other two coordinates. Either ) axis. Unfortunately, there are a number of different notations used for the other two coordinates. Either 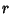 or or  is usedto refer to the radial coordinate and either is usedto refer to the radial coordinate and either  or or  to the azimuthal coordinates. Arfken (1985), for instance,uses to the azimuthal coordinates. Arfken (1985), for instance,uses  , while Beyer (1987) uses , while Beyer (1987) uses  . In this work, the Notation . In this work, the Notation  isused. isused.
where  , ,  , and , and  . In terms of . In terms of 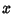 , ,  , and , and 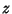
Morse and Feshbach (1953) define the cylindrical coordinates by
where  and and 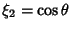 . The Metric elements of the cylindrical coordinates are . The Metric elements of the cylindrical coordinates are
so the Scale Factors are
The Line Element is
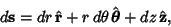 | (16) |
 | (17) |
 | (18) |
 | (19) |
Derivatives of unit Vectors with respect to the coordinates are
 |  |  | (23) | 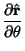 |  |  | (24) |  |  |  | (25) |  |  |  | (26) |  |  |  | (27) |  |  |  | (28) |  |  |  | (29) |  |  |  | (30) |  |  |  | (31) |
The Gradient of a Vector Field in cylindrical coordinates is given by
 | (32) |
 |  |  | (33) |  |  |  | (34) |  |  |  | (35) |  |  |  | (36) |  |  |  | (37) |  |  |  | (38) |  |  |  | (39) |  |  |  | (40) | 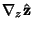 |  |  | (41) |
Now, since the Connection Coefficients are defined by
 | (42) |
The Covariant Derivatives, given by
 | (46) |
 |  |  | (47) | 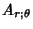 |  |  | | | |  |  | (48) |  |  |  | (49) |  |  |  | (50) | 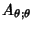 |  | 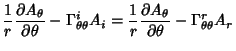 | | | |  |  | (51) |  |  | 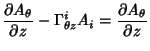 | (52) |  |  |  | (53) |  |  | 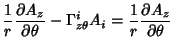 | (54) | 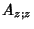 |  |  | (55) |
Cross Products of the coordinate axes are
The Commutation Coefficients are given by
 | (59) |
 | (60) |
 , where , where 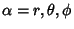 . Also . Also
 | (61) |
 , ,  . Finally, . Finally,
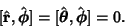 | (62) |
Time Derivatives of the Vector are
Speed is given by
 | (68) |
Cross Products of the axes are
The Convective Derivative is
 | (73) |
 | (74) |
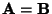 , to obtain , to obtain
 | (75) |
 | (76) |
 | (77) |
 | (78) |
 | (79) |
 , ,
 | (80) |
so, as expected,
 | (84) |
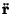 , so combining all three pieces gives , so combining all three pieces gives
The Divergence is
or, in Vector notation
 | (87) |
and the Laplacian is
The vector Laplacian is
 | (90) |
The Helmholtz Differential Equation is separable in cylindrical coordinates and has StäckelDeterminant 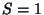 (for (for 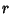 , ,  , , 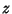 ) or ) or  (for Morse and Feshbach's (for Morse and Feshbach's , ,  , ,  ). ). See also Elliptic Cylindrical Coordinates, Helmholtz Differential Equation--Circular Cylindrical Coordinates, Polar Coordinates, Spherical Coordinates
References
Arfken, G. ``Circular Cylindrical Coordinates.'' §2.4 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 95-101, 1985.Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 212, 1987. Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, p. 657, 1953. |

![]() ) axis. Unfortunately, there are a number of different notations used for the other two coordinates. Either
) axis. Unfortunately, there are a number of different notations used for the other two coordinates. Either ![]() or
or ![]() is usedto refer to the radial coordinate and either
is usedto refer to the radial coordinate and either ![]() or
or ![]() to the azimuthal coordinates. Arfken (1985), for instance,uses
to the azimuthal coordinates. Arfken (1985), for instance,uses ![]() , while Beyer (1987) uses
, while Beyer (1987) uses ![]() . In this work, the Notation
. In this work, the Notation ![]() isused.
isused.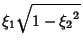














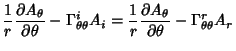

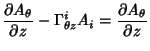

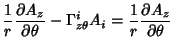




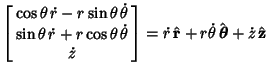



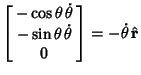

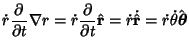







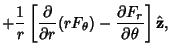
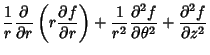
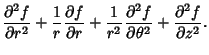

![]() (for
(for ![]() ,
, ![]() ,
, ![]() ) or
) or ![]() (for Morse and Feshbach's
(for Morse and Feshbach's![]() ,
, ![]() ,
, ![]() ).
).