3．函数的幂级数展开式

[幂级数的唯一性定理] 如果函数f(x)(或f(x,y))在x=0(或x=0,y=0)可以展开成幂级数

f(x)=

或                                            

那末这个幂级数就是它的马克劳林级数.

[幂级数的存在性定理]

1° 若函数f (x)在x=0具有任意阶导数，且当≤x≤R时

式中R_n(x)是马克劳林公式的余项，则函数f(x)在区间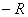≤x≤R上可以展开成幂级数.实际上可以证明，存在由函数f(x)产生的马克劳林级数，它虽然收敛，但它的和却不等于f (x).

2° 若函数f (x,y)在点(0,0)具有任意阶偏导数，且当(x,y)是xy平面上某一区域M上的点时

式中R_n(x,y)是马克劳林公式的余项，则函数f(x,y)在区域M上可以展开成幂级数.

上述理论容易推广到二元以上的多变量函数的情形.