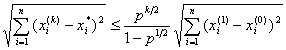§3 线性方程组
一、含n个未知量n个方程的线性方程组的解法
[齐次和非齐次线性方程组] 含n个未知量n个方程的线性方程组取如下形式:
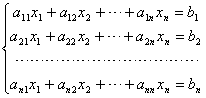 (1)
(1)
当常数项b1,b2,...,bn不全为零时,(1)称为非齐次线性方程组;当b1,b2,...,bn全为零时,(1)称为齐次线性方程组.
如果记
A=(aij)= (系数矩阵)
(系数矩阵)
x=(x1,x2,...,xn)t
b=(b1,b2,...,bn)t (常数项矢量)
式中t表示转置,那末线性方程组(1)可写成矩阵形式
Ax=b (2)
[逆矩阵法] 当ïAï ≠0时,线性方程组(2)的解为
x=![]() b
b
式中![]() 是系数矩阵A的逆矩阵,x称为(2)的解矢量.
是系数矩阵A的逆矩阵,x称为(2)的解矢量.
[克莱姆法则] 若ïAï ≠0,则方程组(1)的解为
![]() ,
, ![]() , ... ,
, ... , ![]()
式中
 ,
, 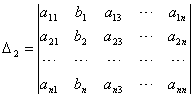 , ... ,
, ... ,
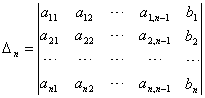
这里Dj(j=1,2,...,n)是以常数项矢量b替换A中第j列矢量后得到的n阶行列式.特别
1° 二阶线性方程组
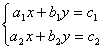
的解为
![]() ,
, ![]()
式中
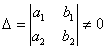 ,
, 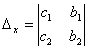 ,
, 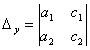
2° 三阶线性方程组
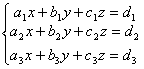
的解为
![]() ,
, ![]() ,
, ![]()
式中
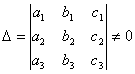 ,
, 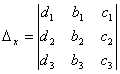
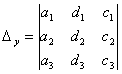 ,
, 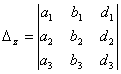
[有回代过程的主元素消去法(高斯消去法)] 对于n阶线性方程组
![]()
可用矩阵表成
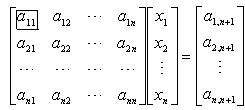
消元步骤:
(1)在系数矩阵中找出绝对值最大的元素(这元素称为主元素),不妨设a11(第1行第1列元素)为主元素,(不然,如果![]() 为主元素,可先将第i个方程与第1个方程互换位置,再把未知数x1和xj的次序调换,那末得到新的系数矩阵,其主元素必在第1行第1列上).将第1个方程乘以
为主元素,可先将第i个方程与第1个方程互换位置,再把未知数x1和xj的次序调换,那末得到新的系数矩阵,其主元素必在第1行第1列上).将第1个方程乘以![]() ,分别与第i个方程相加(i=2,3,...,n),得到新的n阶线性方程组,用矩阵表示如下
,分别与第i个方程相加(i=2,3,...,n),得到新的n阶线性方程组,用矩阵表示如下
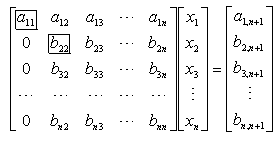
(2)在除第1行外的系数矩阵中找出主元素,不妨设b22为主元素.再将第二个方程乘以![]() 分别与第i个方程相加(i=3,4,...n),得到新的n阶线性方程组,用矩阵表示如下
分别与第i个方程相加(i=3,4,...n),得到新的n阶线性方程组,用矩阵表示如下

(3)按照(1),(2)的方法进行n次以后,在第1至n
行外的系数矩阵

中找出主元素,不妨设![]() 为主元素,将第n
为主元素,将第n![]() 个方程乘以
个方程乘以![]() 与第n个方程相加,得到新的n阶线性方程组,用矩阵表示如下
与第n个方程相加,得到新的n阶线性方程组,用矩阵表示如下
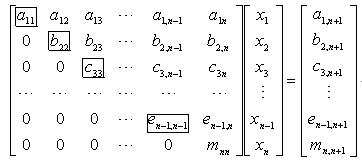
这样做完n![]() 次之后,消元过程结束.原来系数矩阵已经化成上三角形矩阵(这时未知数的次序已做了若干次调换).
次之后,消元过程结束.原来系数矩阵已经化成上三角形矩阵(这时未知数的次序已做了若干次调换).
回代步骤:
由第n个方程解出
![]()
将xn代入第n![]() 个方程,解出
个方程,解出![]() ,再将
,再将![]() , xn代入第n
, xn代入第n![]() 个方程解出
个方程解出![]() ,...,最后将已解出的x2,x3,...,xn代入第一个方程解出x1.
,...,最后将已解出的x2,x3,...,xn代入第一个方程解出x1.
注意,这里每当找出主元素后,都经过行与行互换和未知数次序调换等手续,也可以把调换未知数次序的步骤放到第n-1步之后一起去做,同样可以得到三角形的系数矩阵.
例1 用主元素消去法解方程组

解 方程组用矩阵表示为:
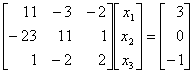
解的步骤如下:
(1)第2 行第1列的元素-23是主元素,用□框起来,并用矩阵表示成

把矩阵第2行乘以![]() 加到第1行上,把第2行乘以
加到第1行上,把第2行乘以![]() 加到第3行上,得到矩阵
加到第3行上,得到矩阵
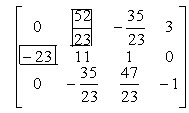
在除第2行外的系数矩阵中找到第二个主元素在第1行第2列上为![]() .
.
(2)把第1行乘以![]() 加到第3行上,得到矩阵
加到第3行上,得到矩阵
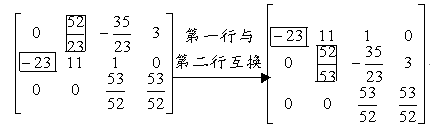
(3)由第三个方程解出![]() ,将
,将![]() 代入第二个方程,解出
代入第二个方程,解出![]() ,将
,将![]() ,
,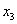 代入第一个方程,解出
代入第一个方程,解出![]() .
.
于是方程组的解为(1,2,1).
[无回代过程的主元素消去法] 这种方法与上法基本一样,不同之处在于每次消元时,都用某一方程去消去其余所有n-1个方程的未知数,例如上面方法的消元步骤(2)中,改成将第二个方程乘以![]() 分别与第i个方程相加,i=1,3,4,...,n(共n-1个,与上面方法不同的是,这里包括i=1,并设a12=b12),得到新的系数矩阵是
分别与第i个方程相加,i=1,3,4,...,n(共n-1个,与上面方法不同的是,这里包括i=1,并设a12=b12),得到新的系数矩阵是
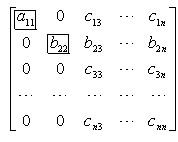
而最后得到对角系数矩阵是:

因此不需经过回代过程,即可直接解出各个未知数来.
无回代过程的主元素消去法运算量比有回代过程的大,但在电子计算机上编制程序较为简单.
为了减少运算量,便于编制程序,第一步可在系数矩阵的第1列找出绝对值最大的元素为列主元素,消元后,第二步从系数矩阵的第2列找出列主元素进行消元,等等.这种消元法称为列主元素消去法,它也可达到较好的精确度.
[简单迭代法] 一般步骤:
(1) 将线性方程组
![]()
改写成
![]()
(2)任意选取一组初始近似值![]() 作为方程的第0次近似解.
作为方程的第0次近似解.
(3)依次使k=1,2,3,...,用公式
![]()
求出方程的第k次近似解,直至满足
![]()
为止,式中e>0为预先给定的允许误差.于是第k次近似解![]() 在允许误差e的范围内满足方程组.注意这里的允许误差不是指近似解与精确解之间的最大绝对误差.
在允许误差e的范围内满足方程组.注意这里的允许误差不是指近似解与精确解之间的最大绝对误差.
- 用简单迭代法求方程组
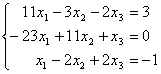
的解,其允许误差![]() .
.
解 根据例1可化为方程组

分别由![]() ,可得迭代方程(满足收敛条件)
,可得迭代方程(满足收敛条件)
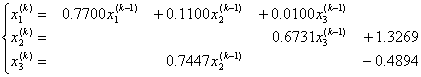
选取初始值![]() ,逐次迭代得出一系列近似解:
,逐次迭代得出一系列近似解:
|
|
|
|
|
|
|
|
|
| 0 | 1 | 1 | 1 | 10 | 0.9581 | 1.9684 | 1.0000 |
| 1 | 0.8900 | 2.0000 | 0.2553 | 11 | 0.9643 | 2.0000 | 0.9764 |
| 2 | 0.9079 | 1.4987 | 1.0000 | 12 | 0.9723 | 1.9841 | 1.0000 |
| 3 | 0.8739 | 2.0000 | 0.6267 | 13 | 0.9769 | 2.0000 | 0.9882 |
| 4 | 0.8992 | 1.7487 | 1.0000 | 14 | 0.9821 | 1.9920 | 1.0000 |
| 5 | 0.8947 | 2.0000 | 0.8129 | 15 | 0.9853 | 2.0000 | 0.9941 |
| 6 | 0.9171 | 1.8741 | 1.0000 | 16 | 0.9887 | 1.9960 | 1.0000 |
| 7 | 0.9223 | 2.0000 | 0.9062 | 17 | 0.9908 | 2.0000 | 0.9970 |
| 8 | 0.9392 | 1.9369 | 1.0000 | 18 | 0.9929 | 1.9980 | 1.0000 |
| 9 | 0.9463 | 2.0000 | 0.9530 | 19 | 0.9943 | 2.0000 | 0.9985 |
迭代19次后得到![]() ,
,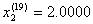 ,
,![]() 在允许误差
在允许误差![]() 范围内满足方程组.
范围内满足方程组.
[赛得尔迭代法] 把简单迭代法的步骤(3)中的迭代公式改成
![]()
其他步骤同简单迭代法.
在一般情况下,赛得尔迭代法比简单迭代法收敛得快些.
- 用赛得尔迭代法求例2中方程组的解.
解 选取初始值![]() ,并代入方程
,并代入方程![]() 计算出
计算出
![]()
再将![]() 代入方程
代入方程![]() 计算出
计算出
![]()
再将![]() 代入方程
代入方程![]() 计算出
计算出
![]()
再将![]() ,按赛得尔迭代法继续迭代可以发现,
,按赛得尔迭代法继续迭代可以发现,![]() 因此只需考虑方程
因此只需考虑方程![]() ,
,
![]()
即解方程![]()
得出![]() ,因此方程组的解为
,因此方程组的解为
![]() ,
,![]() ,
,![]()
[迭代法的收敛条件与误差估计]
| 方法 | 收敛条件 | 第k次近似解 | |
|
简 单 迭 代 法 |
|
| |
|
|
| ||
|
|
| ||
| 赛 得 尔 迭 代 法 |
或
|
其中
| |
[松弛迭代法] 把简单迭代法的迭代公式改成
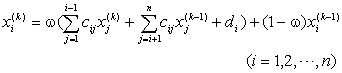
其他步骤同简单迭代法.上式中w 是常数,称为松弛因子.适当选取w 可以提高收敛速度,通常w 取为1.5~2(当取w Î (1,2)时,称为超松弛迭代法,当取wÎ (0,1)时,称为低松弛迭代法).
[共轭斜量法] 线性方程组
Ax=b
可按下面步骤解出:
(1)首先选取适当的近似解为初始值:
![]()
(2)计算初次残差矢量
r(0)=b-Ax(0)
和矢量 p(0)=At r(0)
式中At 为A的转置矩阵.
(3)对i=0,1,2,...,N-1,依次按下列公式迭代
![]()
x(i+1)=x(i)+aip(i)
r(i+1)=r(i)-aiAp(i)
![]()
p(i+1)=At r(i+1)+b i+1p(i)
式中(a,b)表示矢量a和b的内积(见第八章).
这一过程只要进行到r(N)足够小即可停止.
[追赶法解实三对角线性方程组] 实三对角线性方程组
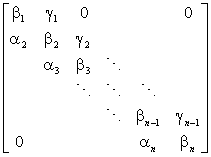
 =
=![]()
可按下面步骤解出:
首先计算
![]() ,
, ![]()
再对k=2,3,...,n-1,依次按下列公式迭代
![]() ,
, ![]()
最后得到线性方程组的解为
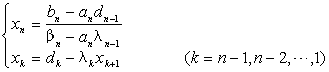
- 用追赶法解方程组
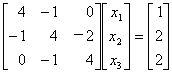
解 按上述公式依次计算得到
![]() ,
, ![]()
 ,
, 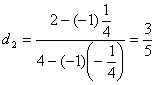
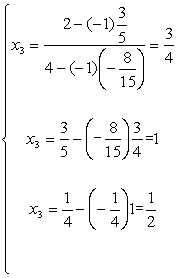
[平方根法解正定矩阵的线性方程组] 设A为正定矩阵,则线性方程组
Ax=b
可按下面步骤解出:
(1)计算lij(分解A=LLt ,L=(lij)为实非奇异下三角形矩阵)
![]()
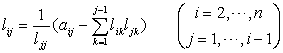
式中n为矩阵A的阶数.
(2)计算yi(解方程组Ly=b)
![]()
(3)计算xi(解方程组Lt x=y)
![]()
[正定带型矩阵的线性方程组解法] 设A=(aij)为一正定带型矩阵,满足
aij=0, ï i-jï >m (m为正整数)
则线性方程组
Ax=b
可按下面步骤解出:
(1) 计算l ij.为了节省存储单元,充分利用矩阵的对称和带型特点,只需存储对角线和对角线下的带中元素,这时可以改变aij的下标,令
aij=ai,m-i+j
例如当n=4,m=2的对称带型矩阵的存储格式为
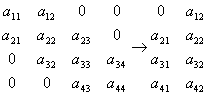
然后按下列公式计算l ij:
当i≤m时,
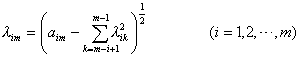
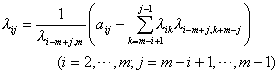
当i>m时,
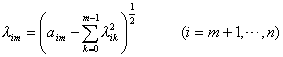

(2)计算yi. 令
lij=l i,m-i+j
且按下列公式计算yi:

![]()
(3)计算xi.
![]()
![]()
这方法只有当m远小于n时才显示出优越性,否则选用其他方法.本公式利用了矩阵的对称性与带型特点,便于在电子计算机上存储,并进行计算.