2 . 含参数广义积分

[一致收敛性]设函数f(x,y)是定义在区域R(a≤x<∞, y₁<y<y₂)上的连续函数，若对任意给定的ε>0，都存在只与ε有关的正数B=B(ε),使得当b≥B时，对区间(y₁，y₂)内一切y不等式

都成立，则称广义积分在区间(y₁，y₂)内一致收敛，并且在该区间内是参数y的连续函数.

[一致收敛判别法]

1°柯西判别积分

在区间(y₁，y₂)内一致收敛的充分必要条件是：对任意ε>0，都存在正数B=B(ε),使得当b'>B,b''>B时，对区间(y₁，y₂)内的一切y,都有

2°外尔斯特拉斯判别法  设函数f(x,y)(x的函数)在任一有限区间[a,A]上可积，若存在与参数y无关的函数F(x)，它在区间[a,∞)上可积，并且对于区间(y₁，y₂)内的一切y

                             |f(x,y)|≤F(x)              (x≥a)

则积分

在区间(y₁，y₂)内一致收敛.

[对参数的微分法]若(i)函数f(x,y)在区域R(a≤x<∞,y₁<y<y₂)内连续，并对参数y可微，(ii)积分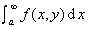收敛，(iii)积分在区间(y₁，y₂)内一致收敛,则当y₁<y<y₂时，

[对参数的积分法]若函数f (x,y)在区域R(a≤x<∞, y₁<y<y₂)内连续 ，并且在区间(y₁，y₂)内一致收敛，则