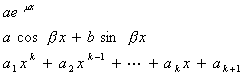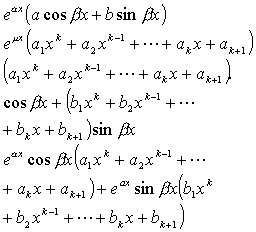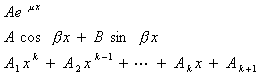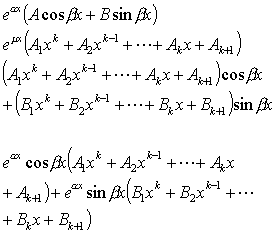2. 非齐次线性微分方程特解的求法

    给定阶非齐次线性微分方程

它的特解可用下面两种方法来求.

    [常数变易法]  设其相应的齐次线性微分方程的通解是

那末非齐次线性微分方程有一个特解

式中是待定函数，它们的导数满足方程组

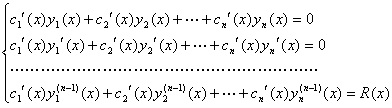
    例  求微分方程

的通解.

    解  先求其相应的齐次方程的通解.

    因特征方程，有特征根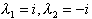.于是齐次方程的通解为

    利用常数变易法求非齐次方程的一个特解y*(x) .令

而c₁(x),c₂(x)由下列方程组确定

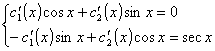
解方程组得

积分后得

（k₁,k₂是任意常数）

（因为只要一个特解，可令k₁=k₂=0）,所以原方程的通解为

[待定系数法]  对特殊类型的，可把特解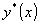的待定表达式及其相应的各阶导数代入原微分方程，然后比较同类项系数，定出的待定表达式里所含的系数，最后得出方程的特解.现在把部分情况下的特解形式列表如下：

    表中为已知常数；是正整数，如果的两个多项式的次数不相同，则取为次数较大者；是待定常数.

    表中右栏表达式分别是（自上而下）在不是其特征根的情形下的特解的待定表达式；如果它们是特征方程的重根，那末在表中的表达式上再乘以.

    例  求解微分方程

    解  先求相应的齐次线性方程y⁽⁴⁾+2y"+y=0的通解.

    由特征方程⁴+2²+1=(²+1)²=0可知特征根=i都是二重根.所以齐次方程的通解为

y(x)=c₁cosx+c₂sinx+c₃x cosx+c₄x sinx

    利用待定系数法，求非齐次线性方程的一个特解.由于R(x)=sin2x，属于表中第二类表达式(a=0,b=1,=2)，同时i=2i不是特征根，所以特解应为y*(x)=Acos2x+Bsin2x.代入原方程，比较同类项系数得

所以特解是                       

原方程的通解为

式中c₁,c₂,c₃,c₄是任意常数.