第八章 第八章 矢量算法与场论初步·张量
算法与黎曼几何初步
本章包括两个部分.
第一部分是矢量代数、矢量分析及其在场论中的应用.主要内容有:矢量的概念、矢量的算法与矢量的坐标表示;以矢量作为工具介绍了场论中的一些基本内容.例如梯度、散度与旋度等基本概念及其计算公式和性质,以及它们在不同坐标系中的表达式;叙述了矢量的积分定理(高斯公式、斯托克斯公式和格林公式);引进了仿射坐标系,阐述了三维空间中的协变矢量和逆变矢量,同时把这些概念推广到n维空间中去.
第二部分是张量代数、张量分析及其在黎曼几何中的应用.介绍了张量的概念和一些张量算法,然后以张量作为工具来阐述仿射联络空间的基本内容.例如,仿射联络、矢量和张量的平行移动,及协变微分法与自平行曲线等;并在n维空间中引进度量的概念,来定义黎曼空间,从而由具有特殊条件的仿射联络引出了黎曼联络,于是有关仿射联络空间中的一些性质可以搬到黎曼空间中来.可是,因为黎曼空间是由度量定义的,所以与度量有关的一些性质在仿射联络空间中是没有的.
§1 矢量算法
一、 一、 矢量代数
[矢量概念] 只有大小的量称为标量(也称为数量或纯量).例如温度、时间、质量、面积、能量等都是标量.
具有大小和方向的量称为矢量(也称为向量).例如力、速度、力矩、加速度、角速度、动量等都是矢量.
在几何中的有向线段就是一个直观的矢量.通常用空间中的有向线段AB来表示矢量.用长度![]() 表示大小,用端点的顺序A
表示大小,用端点的顺序A![]() B表示方向.A称为始点,B称为终点,这个矢量记作
B表示方向.A称为始点,B称为终点,这个矢量记作![]() ,或用黑正体字母a表示.矢量的大小(或长度)的数值称为它的模或绝对值,用记号
,或用黑正体字母a表示.矢量的大小(或长度)的数值称为它的模或绝对值,用记号![]() 或|a|表示.
或|a|表示.
矢量按其效能可分成三种基本类型:
具有大小和方向而无特定位置的矢量称为自由矢量.例如力偶.
沿直线作用的矢量称为滑动矢量.例如作用于刚体的力.
作用于一点的矢量称为束缚矢量.例如电场强度.
在这里所讨论的矢量,除特别说明外,都指自由矢量,就是说,所有方向相同,长度相等的矢量,不管始点如何,都看作相同的矢量.
模等于1的矢量称为单位矢量.
模等于零的矢量称为零矢量,记作0,它是始点和终点重合的矢量.
模与矢量![]() 的模相等而方向相反的矢量称为a的负矢量,记作-a.
的模相等而方向相反的矢量称为a的负矢量,记作-a.
 始点与原点O重合而终点位于一点M的矢
始点与原点O重合而终点位于一点M的矢
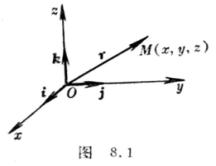
量![]() (图8.1)称为点M的矢径(或向径),记作
(图8.1)称为点M的矢径(或向径),记作
r,原点称为极点.如果M的直角坐标为x,y,z ,
则有
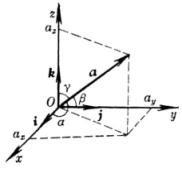
r=![]() =(x,y,z)=xi+yj+zk
=(x,y,z)=xi+yj+zk
式中i,j,k分别为x轴,y轴,z轴的正向单位
矢量,称为坐标单位矢量(或基本矢量).
[矢量的基本公式]
| 名 称 | 公 式 | 图 形 |
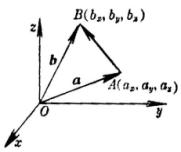
| 矢量a的坐标表示 坐标单位矢量i,j,k 的坐标表示 零矢量的坐标表示 a的长度(或模) a的方向余弦( 为a的方向角) 矢量 B的坐标分别为( ax,ay,az), (bx,by,bz) | a=axi+ayj+azk=(ax, ay, az) i=(1,0,0) j=(0,1,0) k=(0,0,1) 0=(0,0,0)(0无方向) +(bz-az)k |
|
[加法] 若a=(ax,ay,az),b=(bx,by,bz),则
a+b=( ax+bx,ay+by,az+bz)
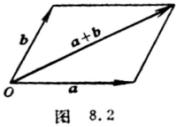
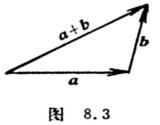 把矢量的始点移到原点O,以a,b为边作平行四边行,由原点作出的对角线就表示和矢量a+b(称为平行四边形法则,见图8.2);或者把二矢量首尾相接,由始点到终点的矢量即为和矢量a+b(称为三角形法则,见图8.3).
把矢量的始点移到原点O,以a,b为边作平行四边行,由原点作出的对角线就表示和矢量a+b(称为平行四边形法则,见图8.2);或者把二矢量首尾相接,由始点到终点的矢量即为和矢量a+b(称为三角形法则,见图8.3).
加法运算适合如下规律: ![]() (交换律)
(交换律)
![]() (结合律)
(结合律)
a+0=0+a=a,a+(-a)=0
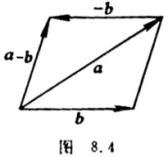
[减法] 若a=(ax,ay,az),b=(bx,by,bz),则
a-b=(ax-bx,ay-by,az-bz)
把矢量b的负矢量与矢量a相加,得矢量a-b
(图8.4).
对任意两个矢量a和b成立三角形不等式:
|a+b||a|+|b|
[数乘] 以实数![]() 乘矢量a称为数乘,记作
乘矢量a称为数乘,记作![]() a.当
a.当![]() >0时,a的模伸缩
>0时,a的模伸缩![]() 倍,方向保持不变;当
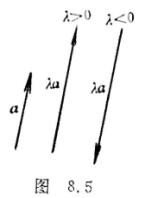
倍,方向保持不变;当![]() <0时,a的模伸缩|
<0时,a的模伸缩|![]() |倍,而方向与a相反(图8.5),如果a=(ax,ay,az)则
|倍,而方向与a相反(图8.5),如果a=(ax,ay,az)则
![]() a=(
a=(![]() ax,
ax, ![]() ay,
ay, ![]() az)
az)
设![]() ,
,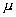 为两实数,a,b为两矢量,则数乘运算适合
为两实数,a,b为两矢量,则数乘运算适合
下列规律:
 (
(![]() a)=(
a)=(![]()
![]() )a (结合律)
)a (结合律)
(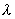 +
+![]() )a=
)a=![]() a+
a+![]() a (分配律)
a (分配律)
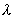 (a+b)=
(a+b)=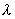 a+
a+![]() b (分配律)
b (分配律)
[矢量的分解]
 1
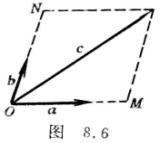
1![]() 设a,b,c为三个共面的矢量,而b和c为非共线矢量,如果把它们移到公共始点O,由矢量c的终点C作两条平行于a,b的
设a,b,c为三个共面的矢量,而b和c为非共线矢量,如果把它们移到公共始点O,由矢量c的终点C作两条平行于a,b的
直线,各交a,b(或延长线)于M,N(图8.6),则
c=![]() +
+![]() =
= ![]() a+
a+![]() b
b
这称为矢量c对a,b的分解.
2![]() 设a,b,c 为非共面矢量,而d为任一矢量,把
设a,b,c 为非共面矢量,而d为任一矢量,把
它们移到公共始点O,由矢量d的终点D作三个平面分别
平行于(b,c)平面,(c,a)平面和(a,b)平面,且与a,b,c(或延长线)分别交于L,M,N(图8.7),则
 d=
d=![]() +
+![]() +
+![]() =
= a+
a+![]() b+
b+![]()
称为矢量d对a,b,c的分解.
3![]() 如果两个非零矢量a与b有线性关系
如果两个非零矢量a与b有线性关系
a+
b=0
式中![]() ,
, ![]() 不全为0,则称这两个矢量共线(即
不全为0,则称这两个矢量共线(即
a//b);反之也真.称这两个矢量a,b为线性相关.
4![]() 设a,b为两个非零矢量,若
设a,b为两个非零矢量,若![]() a+
a+![]() b =0,则有
b =0,则有![]() =0,
=0,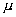 =0,这时称a,b为线性无关.
=0,这时称a,b为线性无关.
5![]() 若三个非零矢量a,b,c有线性关系
若三个非零矢量a,b,c有线性关系![]() a+
a+![]() b+
b+![]() =0,式中
=0,式中![]() ,
,![]() ,
,![]() 不全为零,则这三个矢量共面,反之也真.这时,称a,b,c为线性相关.如果a,b,c为三个非零矢量,而
不全为零,则这三个矢量共面,反之也真.这时,称a,b,c为线性相关.如果a,b,c为三个非零矢量,而![]() a+
a+![]() b+
b+![]() =0,则有
=0,则有![]() =
=![]() =
=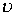 =0,这时,称a,b,c为线性无关.
=0,这时,称a,b,c为线性无关.
6![]() 四个(或四个以上)矢量a,b,c,d必有线性关系;就是说它们一定线性相关.这时,必有不全为0的四个数
四个(或四个以上)矢量a,b,c,d必有线性关系;就是说它们一定线性相关.这时,必有不全为0的四个数![]() ,
,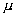 ,
,![]() ,
,![]() ,成立
,成立![]() a+
a+![]() b+
b+![]() +
+![]() d=0.
d=0.
[标量积(数量积、点积、内积)] 设a=(ax, ay, az),b=(bx,by,bz),|a|=a,|b|=b,a,b两矢量的夹角为![]() ,则称数值ab cos
,则称数值ab cos![]() 为矢量a,b的标量积(也称为数量积、点积或内积).记作
为矢量a,b的标量积(也称为数量积、点积或内积).记作
 a·b=ab=ab cos
a·b=ab=ab cos![]() (0
(0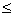
![]()
![]()
![]() )
)
可以看作矢量a的长度乘以矢量b在a上的投影的长度(图8.8).
标量积运算适合以下的规律:
a·b=b·a (交换律)
a·(b+c)=a·b+a·c (分配律)
(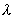 a)·(
a)·(![]() b)=
b)=![]()
![]() a·b (数乘的结合律)
a·b (数乘的结合律)
a·a=a2=|a|2=a2
若a,b为非零矢量,a·b=0,则a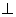 b;反之也真.
b;反之也真.
i·i=j·j=k·k=1,i·j=j·k=k·i=0
a·b=axbx+ayby+azbz (即对应坐标相乘之和)
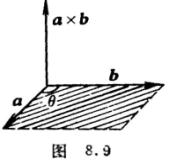
[矢量积(叉积、外积)]设a=(ax,ay,az),b=(bx,by,bz),|a|=a,|b|=b,a,b两矢量的夹角为![]() ,则定义a×b为两矢量的矢量积(也称为叉积或外积),它是一个矢量,即长度等于以a,b为边的平行四边形的面积(图8.9阴影部分)
,则定义a×b为两矢量的矢量积(也称为叉积或外积),它是一个矢量,即长度等于以a,b为边的平行四边形的面积(图8.9阴影部分)
 |a×b|=absin
|a×b|=absin![]() (0
(0![]()
![]()
![]()
![]() )
)
它的方向垂直于两矢量a和b,并且a,b,a×b构成
右手系(图8.9).
矢量积运算适合下列规律:
a×b=-b×a (反交换律)
(a+b)×c=a×c+b×c (分配律,次序不能交换)
( a)×(
a)×(![]() b)=
b)=![]()
![]() (a×b)
(a×b)
[(![]() +
+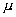 )a]×b=(
)a]×b=(![]() +
+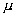 )(a×b)=
)(a×b)= (a×b)+
(a×b)+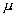 (a×b)
(a×b)
a×a=0
若a,b为非零矢量,则a,b共线(即a//b)的充分必要条件是:
a×b=0
i×i=j×j=k×k=0,i×j=k,j×k=i,k×i=j
a×b= =(ay bz- az by)i+( az bx-ax bz)j+( ax by-ay bx)k
=(ay bz- az by)i+( az bx-ax bz)j+( ax by-ay bx)k
[两矢量的夹角]
cos(a,b)=![]()
sin(a,b)=![]()
[拉格朗日恒等式]
(a×b)·(c×d)=(a·c)(b·d)-(a·d)(b·c)
特别 (a×b)2=a2b2-(ab)2
即 (ay bx- az by)2+( az bx-ax bz)2+( ax by-ay bx)2
=(ax2+ay2+az2)(bx2+by2+bz2)-(axbx+ayby+azbz)2
[三个矢量的混合积] 设a=(ax,ay,az),b=(bx,by,bz),c=(cx,cy,cz)为三个矢量,则它们的混合积定义为
(abc)=a·(b×c)=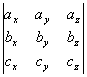 =ax(bycz-bzcy)+ay(bzcx-bxcz)+az(bxcy-bycx)
=ax(bycz-bzcy)+ay(bzcx-bxcz)+az(bxcy-bycx)
混合积具有性质:
1![]() a·(b×c)=(a×b)·c
a·(b×c)=(a×b)·c
注意,一般情况下等式
(a·b)·c =a·(b·c)
(a×b)×c =a×(b×c)
不成立.
2![]() (abc)=(bca)=(cab)=-(acb)=-(bac)=-(cba)
(abc)=(bca)=(cab)=-(acb)=-(bac)=-(cba)
即有轮换性:
a·(b×c)=b·(c×a)=c·(a×b)=-a(c×b)=-b(a×c)=-c(b×a)
3![]() 混合积(abc)是一个数,它的绝对值等于以a,b,c为边的平行六面体的体积.
混合积(abc)是一个数,它的绝对值等于以a,b,c为边的平行六面体的体积.
4![]() 三个矢量共面的充分必要条件是:(abc)=0.
三个矢量共面的充分必要条件是:(abc)=0.
[三重矢积]
a×(b×c)=(a·c)b-(a·b)c
(a×b)×c=(a·c)b-(b·c)a
采用a,b,c轮换法还可推出其余两个同类公式.
[多重积的几个公式]
a×(b×c)+b×(c×a)+c×(a×b)=0
(a×b)·(c×d)=![]() =(a·c)(b·d)-(a·d)(b·c)
=(a·c)(b·d)-(a·d)(b·c)
(a×b)×(c×d)=(abd)c-(abc)d=(cda)b-(cdb)a
a×[b×(c×d)]=(b·d)(a×c)-(b·c)(a×d)
(a×b b×c c×a)=(abc)2
(a1a2a3)(b1b2b3)=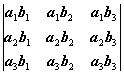
(a×b c×d e×f)=(abd)(cef)-(abc)(def)