二、线性变换的运算
[线性变换的和与数乘] 从空间V到空间![]() 的线性变换的集,记作
的线性变换的集,记作
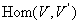
设![]() ,按照下列公式定义
,按照下列公式定义![]() :
:
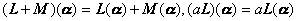
这两个新的变换都是线性的,并且
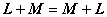
![]() 分别称为线性变换的和与数乘.
分别称为线性变换的和与数乘.
按上面定义的线性变换的和与数乘,集![]() 组成F上的线性空间. 它的维数等于V和
组成F上的线性空间. 它的维数等于V和![]() 的维数n和m的积
的维数n和m的积![]() .
.
[线性变换的乘积] 设![]() 为三个线性空间,若
为三个线性空间,若![]() ,
,![]() 则定义
则定义
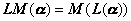
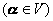
显然![]() 是从
是从![]() 的线性变换,称
的线性变换,称![]() 为线性变换的乘积.
为线性变换的乘积.
线性变换的乘积满足:
1o分配律 若![]() 则
则
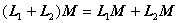
2o结合律 若![]() .
.
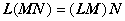
[幂等变换] 如果L是线性空间V到自身的线性变换,满足等式
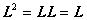
那末称L为幂等变换.
[同构与自同构] 若线性变换![]() 是一对一的,则称L是同构,或称L是正则的. V到自身的一个同构称为自同构. 若V到自身的线性变换不是自同构,则称它为奇异线性变换,否则就称为非奇异线性变换(或正则自同态).
是一对一的,则称L是同构,或称L是正则的. V到自身的一个同构称为自同构. 若V到自身的线性变换不是自同构,则称它为奇异线性变换,否则就称为非奇异线性变换(或正则自同态).
同构有以下性质:
1o![]() 是一个同构的充分必要条件是:
是一个同构的充分必要条件是:
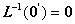
2o若L和M是同构的,![]() ,
,![]() 则
则
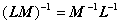
特别,对自同构![]() ,上式也成立.
,上式也成立.
3o域F上线性空间V的一切自同构所成的集G在乘法之下构成一个群. 称G为V的线性变换群,记作![]() ,其中n为V的维数.
,其中n为V的维数.
4o域F上线性空间V的一切线性变换(自同态)所成的集R在加法和乘法之下构成一个环,称R为A的线性变换环.