4. 里兹方法在特征值问题上的应用
算子方程
Au-u=0
的非零解称为算子A的特征值,对应的非零解u称为所对应的特征函数.
对线性算子A,若存在常数K,使对任何MA的元素成立
(A![]() ,
,![]() )≥K||
)≥K||![]() ||2
||2
则称A为下有界算子,正定算子是下有界的(此时K=0).记(A![]() ,
,![]() )/||
)/||![]() ||2的下确界为d.
||2的下确界为d.
定理1 设A为下有界对称算子,若存在不为零的元素0MA,使
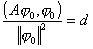
则d就是A的最小特征值,![]() 0为对应的特征函数.
0为对应的特征函数.
于是求下有界对称算子的最小特征值问题化为变分问题,即在希尔伯特空间中求使泛函(A![]() ,
,![]() )/||
)/||![]() ||2取极小的元素,或在||
||2取极小的元素,或在||![]() ||=1的条件下求使泛函(A
||=1的条件下求使泛函(A![]() ,
,![]() )取极小的元素.
)取极小的元素.
定理2 设A是下有界对称算子,![]() 1≤
1≤![]() 2≤…≤
2≤…≤![]() n是它的前n个特征值,
n是它的前n个特征值,![]() 1,
1,![]() 2,…,
2,…,![]() n是对应的标准正交特征函数,如果存在不为零的元素
n是对应的标准正交特征函数,如果存在不为零的元素![]() ,在附加条件
,在附加条件
(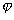 ,
,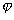 )=1, (
)=1, (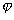 ,
,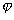 1)=0, (
1)=0, (![]() ,
,![]() 2)=0, …, (
2)=0, …, (![]() ,
,![]() n)=0
n)=0
下使泛函(A![]() ,
,![]() )取极小,则
)取极小,则![]() n+1是算子A的特征函数,对应的特征值
n+1是算子A的特征函数,对应的特征值
![]()
就是除![]() 1
1 ![]() ,
,![]() n外的最小的一个特征值.
n外的最小的一个特征值.
于是求第n+1个特征值就化为变分问题,即在附加条件
(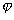 ,
,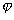 )=1, (
)=1, (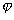 ,
,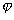 1)=0, (
1)=0, (![]() ,
,![]() 2)=0
2)=0![]() , (
, (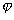 ,
,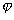 n)=0
n)=0
下求使泛函(A![]() ,
,![]() )取极小的元素.
)取极小的元素.
为了利用里兹方法求特征值,在MA中选取一列在H0中完备的坐标元素序列{i}, (i=1,2![]() ), 令
), 令![]() ,确定ak,使在条件 (un,un)=1下,(Aun,un)取极小,这个问题化为求n个变元a1,a2,…,an的函数
,确定ak,使在条件 (un,un)=1下,(Aun,un)取极小,这个问题化为求n个变元a1,a2,…,an的函数
![]()
在条件
![]()
下的极值问题,一般可用拉格朗日乘数法解(见第九章§3,t),此时
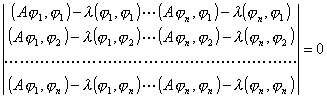
的最小的根即为特征值的近似值,如果将上式的根按大小排列,就依次得后面的特征值的近似值,但精确度较差.
对一般算子方程
Au-Bu=0
如果A为下有界对称算子,B为正定算子,则
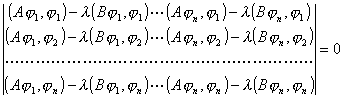
的根就是特征值的近似值.