§4 拟协调单元
一、 一、 协调问题与拟协调单元
等参数单元有一个缺点，就是节点与插值次数无论如何增加，各单元之间都只能保证插值函数本身的连续性，这对于积分式仅含待定函数及其一阶导数的变分问题（例如空间弹性力学问题，其变形能中应变是位移的一阶偏导数）来说是适用的，但是对于包含高阶导数的变分问题（例如杆、板的弯曲问题，其变形能积分就含有待定的挠度函数的二阶偏导数），对插值函数往往要求在整个区域有一阶的连续性。而这类所谓协调问题，等参数单元是无法解决的。这种光滑性的要求当然要首先在节点上反映出来，也就是说，单元的节点参数值应当包含待定函数的有关导数值。这一类单元可统称为拟协调单元。
[型函数] 假定在某个单元
上有p个节点，其局部编号为i=1,2,…,p。先考虑待定函数u=u(x,y,z)及其一阶偏导数在节点i的参数值
每一节点参数值个数r=4。于是每个单元共有4p个节点参数值。如果插值函数
为三元n次多项式
，则其项数或各项系数一般有
个，显然次数n必须满足
这时对应于各节点参数值
，可定义型函数为如下的4p个n次多项式
(i=1,2,…,p) :
（i）（i）在节点i
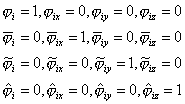
（ii）（ii）在其余p-1个节点j≠i，上述十六个函数即
及其一阶偏导数都等于零。
（iii）（iii）
如果能把这些型函数构造出来，那末u的插值多项式
就可以表示为
如果待定函数是（u,v,w），其他条件同前，则其插值函数（
）可表示为
或用矢量表示
[待定系数法] 待定系数法是从4p个节点参数值直接解出插值多项式的各项系数。一般地说，完全的n次多项式系数{
}的个数N=
会大于4p，需要对多项式补加N-4p个条件才能唯一地确定这些系数。最简单的方式是象§3中那样，限制多项式的形式（例如限制多项式为三k次多项式，即对x、y或z都是k次的，系数的个数就减为
）或除去某些高次项（即令相应的系数
为零）使得系数个数为4p，假定经过限制后的插值多项式改写为
从4p个节点参数值可得4p个方程
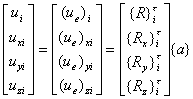（i=1,2,…,p）
式中
等分别表示由多项式各项（项数为4p）及其偏导数在节点i的数值所构成的列矢量。把这单元的全部节点参数值排成列矢量
，并以U表示上式右端p个4×4p的系数矩阵依序排列所构成的4p×4p的系数矩阵，则4p个方程可简写为
从此可解出各项的系数
(15)
可以看出，在同样的限制下，型函数的各项系数实际上就是
中一个分量取1，其余分量取零的解。
另一种方式是对插值函数一般表达式
按光滑性要求或物理条件附加一定的约束，并假定这些约束可表示为N-4p个关于
的线性方程
(16)
式中Q为（N-4p）×N的系数矩阵。对于这完全的n次插值多项式，同样可从4p个节点参数值得出如下4p个方程
(17)
式中
表示4p×N的系数矩阵，只要选取约束条件适当
,
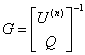
把N×N矩阵G分成前4p列与后（N-4p）列二子矩阵：G=[
]。则
(15)(15)或(17)表示u的节点参数值与插值多项式的系数之间的对应关系，对待定函数v，w也有类似的关系式。如果写成矢量形式，则插值多项式为
(18)
[广义节点参数] 如果直接用插值多项式(18)代替(1)式作单元分析,则变分方程(2)应改为
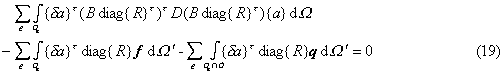
式中各项{R}相当于型函数,而系数{a}起着节点参数值
的作用,称为单元的广义节点参数.在上式和号后的单元系数矩阵与等价外力也是广义的,分别记作
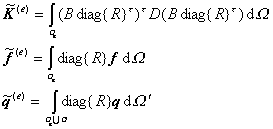
于是有
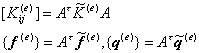
式中A为(15)中的矩阵.对于插值多项式
也有类似结果.
[节点参数值的变换] 节点参数值
中含有偏导数,它们在直角坐标系和局部坐标系中的数值是不同的.例如,直角坐标系中的节点参数值
在局部坐标系中为
(20)
式中四阶矩阵右下标i表示在节点i的值.反之
记局部坐标系中的型函数为
,直角坐标系中的型函数为
,从表达式
可知它们具有如下的线性关系
(21)
实际上,凡是包含微分运算的部分,例如在
的积分式中包含微分运算的矩阵B,边界的方向导数等等,在坐标变换下都要作相应的变换.
