§4  酉空间

一、一、酉空间的定义与性质

    [酉空间与欧氏空间] 设V为一个复数域F上的线性空间，若在V中定义了两个矢量的内积（数量积），记作（），且满足：

(i) （）=（），其中（）是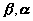（）的共轭复数；

(ii) 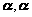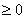（），等号当且仅当时成立；

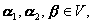
(iii) ，对任意成立；

则称V为一酉（U）空间，又称为内积空间.

若F是实数域，这时内积是可交换的. 有限维实酉空间称为欧氏空间.

例  n维线性空间中，若规定

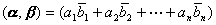
     式中 

则是一个酉空间.

酉空间Ｖ中的内积具有性质：

1^o（）＝

2^o

3^o 一般，则

4^o

[模(范数)]  由于，所以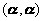是实的. 令

称它为酉空间Ｖ中矢量的模或范数. 模为１的矢量称为单位矢量或标准矢量.

设α，β为酉空间的矢量，c为一复数，则

1^o

2^o    （柯西-施瓦兹不等式）

等号当且仅当α和β线性相关时成立.

3^o

这些性质与空间的维数无关.

[正交与标准正交基]  酉空间V中，若，则称矢量α正交于β. 显然，若α正交于β，则β也正交于α.

酉空间中，任意一组两两正交非零矢量是线性无关的.

如果一组单位矢量两两正交，则称它为一个标准正交组. 若这矢量组又生成整个空间V，则称它为V的标准正交基.

设{}为酉空间V的一组标准正交矢量，，则

1^o     （贝塞耳不等式）

2^o正交于

3^o当V是有限维空间时，{}成为V的基底的充分必要条件是：任一个矢量可表示为

且                

[子空间的正交补空间]  设V为复数域上的酉空间，S为V的一个子空间，若

(i)

(ii) 对和有
则称T为S的正交补空间.

由(i)立刻可知（空集）.

若S是一个有限维酉空间的一个子空间，则中有一个子空间T为S的正交补空间.