§3 无条件极值问题解法
本节讨论目标函数
的极小值问题。设
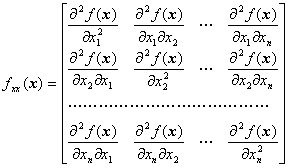
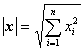
[最速下降法] 迭代程序如下:
(1) (1) 选取初始点
及判别收敛的正数
。
(2) (2) 命
(3) (3) 计算
(4) (4) 命
,若
,则迭代停止,
即为所求;否则进行(5)。
(5) (5) 求
,使
(6) (6) 命
;命
,进行(3)。
这个方法虽然很简单，但点列
收敛于最优解的速度较慢。
[牛顿法] 迭代程序如下：
(1) (1) 选取初始点
及判别收敛的正数
。
(2) (2) 命
(3) (3) 计算
。
(4) (4) 命
若
则迭代停止,
即为所求;否则进行(5)。
(5) 求
使
(6) 命
;命
,进行(3)。
牛顿法虽然可以很快地收敛于最优解,但往往计算逆矩阵
很困难。为了避免此困难,产生了收敛速度介于最速下降法与牛顿法之间的共轭梯度法。
[共轭梯度法]
1o 目标函数是二次函数
的情形,其迭代程序如下:
(1) 选取初始点
及判别收敛的正数
,若
,则迭代停止;否则进行(2)。
(2) (2) 命
,
(3) (3) 算出
(4) (4) 命
(5) (5) 若
,则迭代停止;否则命
命
,进行(3)。
对二次函数只要有限步就可到达最优点。
2o 目标函数是一般函数的情形,其迭代程序如下:
(1) 选取初始点
及判别收敛的正数
。若
,则迭代停止;否则进行(2)。
(2) 命
,
。
(3) 求
使 
(4) 命
(5) 若
,则迭代停止;否则,若
,则
,进行(1),若
,则算出
命 
命
,进行(3)。
这个方法的程序较简单,存储量较小,但当
较小时,计算
可能引起因舍入误差较大而不稳定的情况。
对一般(非二次)函数,这个方法不一定是有限步到达最优解。
[变尺度方法]
1° 目标函数是二次正定函数
的情形,其迭代程序如下:
(1) (1) 选取初始点
及判别收敛的正数
。若
,则迭代停止;否则进行(2)。
(2) (2) 命
,
(
阶单位矩阵),
。
(3) (3) 命
。
(4) (4) 算出
(5) (5) 命
(6) (6) 若
,则迭代停止;否则,命
算出
再进行(7)。
(7) (7) 命
进行(3)。
对二次函数只要有限步就可到达最优点。
2° 目标函数是一般函数的情形,其迭代程序如下:
(1) (1) 选取初始点
及判别收敛的正数
。若
,则迭代停止;否则进行(2)。
(2) (2) 命
,
,
(
阶单位矩阵)。
(3) (3) 命
。
(4) (4) 求
,使
。
(5) (5) 命
。
(6) (6) 若
,则迭代停止;否则,若
,则
,进行(1),若
,则算出
,
,
命
,进行(3)。
对一般(非二次)函数,这个方法不一定是有限步到达最优解。
变尺度法是共轭梯度法的改进,它的收敛速度较快。
[高斯-牛顿最小二乘法] 假设目标函数是平方和的形式
式中
为
维列矢量
。
这是数据处理中最常见的一种函数形式。
显然,如果
的极小点
满足
(
是预先给定的精度),那末可以认为
是方程组
的解。所以最小二乘法也可用来求非线性方程组的解。
函数
一般是非线性的,假设有连续的一阶偏导数:
迭代程序如下:
(1) (1) 选择一初始点
。
(2) (2) 算出
式中
称为对初始值
的校正量;又
假设矩阵
的列矢量为线性独立的,因此逆矩阵
存在。
(3) (3) 命
则
为函数
的极小点的首次近似。
(4) (4) 以
代替前面的
,
代替
,重复上述计算过程,直到
或
为止,在此
和
为预先指定的表示对精确度要求的两个正数。
[改进的高斯-牛顿最小二乘法] 上述高斯-牛顿最小二乘法利用了目标函数为平方和的特点,用
近似代替牛顿法中
的二阶导数矩阵,大大节省了计算量,但是它对初始点
的要求比较严格,如果初始点
与极小点
相距太远,这个算法往往失败。其原因可以从两个方面来看,其一是上述算法基于线性逼近,但在
远离极小点时,这种线性逼近无效;其二是
的最大特征值与最小特征值的比很大,以致使解
变得无意义。为此采取下述改进的办法。
在求出
的校正量
后,不把
作为第
次近似,而将
作为下一步的搜索方向,这时求
使
极小值
然后令
以
代替
重复上述过程,直到
或 
时为止,这时极小点和极小值分别为
,
称
为第
步的最优步长因子。