四、无穷乘积

[基本概念] 设

是一个给定的无穷序列,则记号

=,    q_n≠0 (n=1,)

称为无穷乘积.

称为部分乘积.如果当n→∞时部分乘积序列{P_n}具有有穷的或无穷的（但有确定的正号或负号）极限

P_n=P

则P称为无穷乘积的值，记作

P==,  q_n≠0(n=1,)

若无穷乘积具有非零有穷值P,则称为收敛的，否则称为发散的.若P=0，则称为发散于零.

为使无穷乘积的值等于零，只要乘积的因子中有一个是零就够了，在后面的讨论中，总是假定q_n≠0(n=1,).

称为无穷乘积的余乘积.

[无穷乘积收敛判别法]

(1) 无穷乘积收敛的一个必要条件是：

π_m=1或q_n=1

式中π_m=.

(2) 无穷乘积收敛的充分必要条件是：级数收敛.设L是前面级数的和，则P=e^L.

(3) 设q_n=1+a_n(n=1,2,…)，对充分大的n，若有a_n>0(或a_n<0)，则=收敛的充分必要条件是：级数收敛.

(4) 若级数与级数同时收敛，则=收敛.

(5) 无穷乘积或具有零值的充分必要条件是：级数或的和为.

特别，如果a_n<0且级数发散，或级数收敛而级数发散，那末无穷乘积具有零值.

(6) 无穷乘积绝对收敛的充分必要条件是：级数绝对收敛.

[函数项无穷乘积的一致收敛] 如果函数序列

P_m(x)=         (m=1,)

一致收敛，并且极限不恒为零，那末称函数项无穷乘积

一致收敛.

如果在某一区间上一致收敛，且,那末无穷乘积也在该区间上一致收敛.

[无穷乘积展开式]

     (| x| <1)

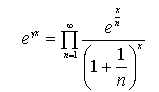(其中γ为欧拉常数)

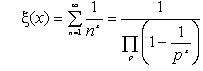
（其中p跑遍一切素数，ξ(x)称为黎曼ξ函数.）