七、泰勒公式与泰勒级数
1. 单变量函数的泰勒公式
[泰勒局部公式] 如果函数f(x)满足条件:(i)在点a的某邻域
内有定义,(ii)在此邻域内有一直到
阶的导数
,
,(iii)在点a处有n阶导数
,那末f(x)在点a的邻域内可表成以下各种形式:
1° f (a+h)=f (a)+
=
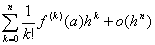(当h→0)
2° f (x)=f (a)+
=
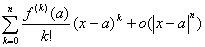(当x→a)
特别,当a=0时,有
[马克劳林公式]
f (x)=f (0)+
=
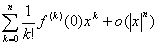(当x→0)
[泰勒公式] 如果函数f (x)满足条件:(i)在闭区间[a,b]上有定义,(ii)在此闭区间上有一直到n阶的连续导数
,(iii)当a<x<b时有有限导数
,那末f(x)在闭区间[a,b]上可表成以下各种形式:
1° f(a+h)= 
(a<a+h<b)
式中 Rn(h)=
(0<θ<1) (拉格朗日型余项)
或 Rn(h)=
(0<θ<1) (柯西型余项)
2° f(x)=
(
)
式中 Rn(x)=
(a<ξ<b) (拉格朗日型余项)
或 Rn(x)=
(0<θ<1) (柯西型余项)
特别,当a=0时,有
[马克劳林公式]
f(x)=
(
)
式中 Rn(x)=
(a<ξ<b) (拉格朗日型余项)
或 Rn(x)=
(0<θ<1) (柯西型余项)
[泰勒级数] 在带余项的泰勒公式2°中,如果把展开式进行到(
)的任意高的乘幂,则有
f(x)=f(a)+
不论它是否收敛,以及它的和是否等于f(x),都称它为函数f(x)的泰勒级数.(
)的乘幂的系数
f(a),
,
,…,
,…
称为泰勒系数.
[马克劳林级数] 在带余项的马克劳林公式中,如果展开式进行到x的任意高的乘幂,则有
f(x)=f(0)+
不论它是否收敛,以及它的和是否等于f(x),都称它为函数f(x)的马克劳林级数.x的乘幂的系数
f (0),
,
,…,
,…
称为马克劳林系数.
多项式的泰勒公式(秦九韶法)见第三章,§2,一.