§2多变量函数极值问题解法(直接法)
本节讨论求目标函数
![]()
在定义区域![]() 上的最优解的直接方法(或试验最优化方法),其中
上的最优解的直接方法(或试验最优化方法),其中
![]() (
(![]() 表示矢量的转置)
表示矢量的转置)
表示自变量![]() 组成的列矢量,由于极小和极大只是目标函数相差一符号,因此这里只讨论求
组成的列矢量,由于极小和极大只是目标函数相差一符号,因此这里只讨论求![]() 维列矢量
维列矢量![]() 使得
使得
![]()
这时,![]() 称为最优解(最优点)。
称为最优解(最优点)。
[单峰函数] 如果函数![]() 在所讨论的区域
在所讨论的区域![]() 上只有一个极值点(最大点或最小点),那末称这个函数为多变量单峰函数。
上只有一个极值点(最大点或最小点),那末称这个函数为多变量单峰函数。
多变量单峰函数也可用分析定义。例如,设函数![]() 定义在区域
定义在区域![]() 上,由于区域
上,由于区域![]() 上的任一路线都可用一参数方程
上的任一路线都可用一参数方程
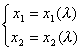
![]()
表示,所以函数![]() 沿这条路线也可用参数
沿这条路线也可用参数![]() 表示为
表示为
![]()
设 ![]()
![]()
又设 ![]()

如果 ![]() ,当
,当![]()
![]() ,当
,当![]()
那末称函数![]() 在区域
在区域![]() 上从点
上从点![]() 和点
和点![]() 的路线上是单峰的,式中
的路线上是单峰的,式中![]()
设 ![]()
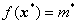
如果对区域![]() 上的任一对点
上的任一对点![]() 和
和![]() ,都存在一条从
,都存在一条从![]() 经过
经过![]() 到
到![]() 的路线,在其上函数
的路线,在其上函数![]() 是单峰的,那末称函数
是单峰的,那末称函数![]() 在区域
在区域![]() 上为单峰的.
上为单峰的.
[因素交替法] 这个方法是轮流按坐标轴方向探索最优点.设![]() 为第i个坐标轴的单位矢量,即
为第i个坐标轴的单位矢量,即
![]()
![]()
并且预先给定允许误差![]() 那末,迭代程序如下:
那末,迭代程序如下:
(1) 选取初始点![]() .
.
(2) 由初始点![]() 出发,先沿第一个坐标轴方向进行优选(用§1的单因素方法),得到好点
出发,先沿第一个坐标轴方向进行优选(用§1的单因素方法),得到好点![]() ,即
,即
![]()
式中![]() 为实参数.然后以
为实参数.然后以![]() 为起点沿第二个坐标轴方向进行优选,得到好点
为起点沿第二个坐标轴方向进行优选,得到好点![]() ,即
,即
![]()
如此等等,一直到![]() 个方向全部优选完毕,得到
个方向全部优选完毕,得到![]() ,它满足
,它满足
![]()
(3) 再以![]() 为新的初始点,重复步骤(2)。
为新的初始点,重复步骤(2)。
(4) 以上步骤一直进行到从某一初始点出发,经过![]() 个方向搜索后得不到新点,或与前
个方向搜索后得不到新点,或与前![]() 个初始点之间的距离都小于预先给定的允许误差
个初始点之间的距离都小于预先给定的允许误差![]() 为止。这时
为止。这时![]() 即为最优点
即为最优点![]() 的近似解。
的近似解。
[平行线法] 如果处理的双因素问题中,有一个因素难于调整,而另一个因素却容易变动,这时用双因素交替法就不太方便,应改用下面的平行线法:
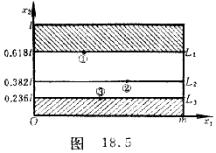 把难于调整的因素
把难于调整的因素![]() 放在纵轴上(图18.5),设其可调范围为[0,
放在纵轴上(图18.5),设其可调范围为[0,![]() ],把容易变动的因素
],把容易变动的因素![]() 放在横轴上,设其可调范围为[0,
放在横轴上,设其可调范围为[0,![]() ].先把因素
].先把因素![]() 固定在点
固定在点![]() 处,在过这点而平行于横轴的直线
处,在过这点而平行于横轴的直线![]() 上对因素
上对因素![]() 在[0,
在[0,![]() ]上优选,好点为①;再把
]上优选,好点为①;再把![]() 固定在点
固定在点![]() 处,在过这点而平行于横轴的直线
处,在过这点而平行于横轴的直线![]() 上对因素
上对因素![]() 在[0,
在[0,![]() ]上优选,好点为②;比较①与②两点的好坏,如果②比①好,就去掉直线
]上优选,好点为②;比较①与②两点的好坏,如果②比①好,就去掉直线![]() 的上半部(如果①比②好,就去掉直线
的上半部(如果①比②好,就去掉直线![]() 的下半部),然后把因素
的下半部),然后把因素![]() 固定在可调范围的
固定在可调范围的![]() 处,在过这点而平行于横轴的直线
处,在过这点而平行于横轴的直线![]() 上对因素
上对因素![]() 在[0,
在[0,![]() ]上优选,好点为③;比较②与③两点的好坏,如果②比③好,就去掉直线
]上优选,好点为③;比较②与③两点的好坏,如果②比③好,就去掉直线![]() 的下半部
的下半部![]() 如此继续做下去把优选范围不断缩小,就可以找到最优点的近似解。
如此继续做下去把优选范围不断缩小,就可以找到最优点的近似解。
对因素![]() 的选择也可采用分数法。
的选择也可采用分数法。
[瞎子爬山法] 迭代过程如下:
(1) (1) 选取初始点(基点)![]() 的步长
的步长![]() ,命
,命![]() 。
。
(2) (2) 进行第k阶段的第l次方向(即![]() 轴方向)的局部探索
轴方向)的局部探索
![]()
其中![]() 为第l个坐标轴的单位矢量,首先沿正方向探索
为第l个坐标轴的单位矢量,首先沿正方向探索
如果![]() ,则探索成功,就把这点作为下一次沿第l+1个坐标轴方向探索的起点,并命
,则探索成功,就把这点作为下一次沿第l+1个坐标轴方向探索的起点,并命![]() ;否则就沿反方向搜索
;否则就沿反方向搜索
![]()
如果![]() ,则探索成功,就把这点作为下一次沿第l+1个坐标轴方向探索的起点,并命
,则探索成功,就把这点作为下一次沿第l+1个坐标轴方向探索的起点,并命![]() ;如果正反方向探索都失败就退回原处,即命
;如果正反方向探索都失败就退回原处,即命
![]()
并命![]() 。
。
当沿各个坐标轴方向的局部探索都轮流进行后,这个阶段的局部探索也就完成了,这时得到第k阶段的最好点![]() 。
。
(3) (3) 命![]() ,以
,以![]() 为新基点,重复步骤(2),如果不能得到更好的点,就缩小步长再进行局部探索,直到步长缩小到规定的精度为止,这时所得最好点即为最优点
为新基点,重复步骤(2),如果不能得到更好的点,就缩小步长再进行局部探索,直到步长缩小到规定的精度为止,这时所得最好点即为最优点![]() 的近似解。
的近似解。
瞎子爬山法(也称探索爬山法)虽然没有前面几个方法快,但它特别适用于因素不能大幅度调动,或是在大生产中如果出一次废品就造成很大损失的情况。
 [陡度法与对角线法]
[陡度法与对角线法]
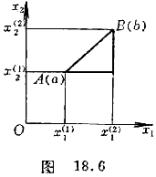
1° 陡度和陡度法 设在![]() ,
,![]() 两点已经做试验,其目标函数值分别为
两点已经做试验,其目标函数值分别为![]() (图18.6),而且
(图18.6),而且![]() ,那末
,那末
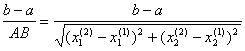
称为从![]() 上升到
上升到![]() 的陡度.对
的陡度.对![]() 维空间有类似的定义。
维空间有类似的定义。
陡度大的方向目标函数显然上升得快一些.所谓陡度法,就是利用已得的试验结果,算出各点间的陡度,然后沿陡度最大的方向(有利方向)再取点做试验。
 2° 联合法(瞎子爬山法与陡度法联合使用) 例如用瞎子爬山法从
2° 联合法(瞎子爬山法与陡度法联合使用) 例如用瞎子爬山法从![]() 点出发,沿
点出发,沿![]() 轴方向调动因素
轴方向调动因素![]() 得到点
得到点![]() ,效果较好,仍沿
,效果较好,仍沿![]() 轴方向调动因
轴方向调动因
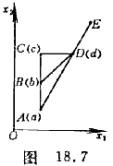
素![]() 得到点
得到点![]() (图18.7),效果还是好的,然后沿
(图18.7),效果还是好的,然后沿![]() 轴方向
轴方向
调动因素![]() 得到点
得到点![]() ,效果也好,接下去就不一定从
,效果也好,接下去就不一定从![]() 出
出
发再沿纵横方向去探索了。这时可以分别算出目标函数由
![]() 上升到
上升到![]() 的陡度,由
的陡度,由![]() 上升到
上升到![]() 的陡度,由
的陡度,由![]() 上升到
上升到![]()
的陡度,从中选出一个陡度最大的方向,例如![]() ,那末
,那末
下一次就可以沿![]() 的方向往上爬了,这时可以从
的方向往上爬了,这时可以从![]() 点出
点出
发沿线段![]() 的延长线
的延长线![]() 用瞎子爬山法往上爬,也可以在
用瞎子爬山法往上爬,也可以在
![]() 上应用单因素的方法优选,一般总可以找出一个比
上应用单因素的方法优选,一般总可以找出一个比![]() 好的点.
好的点.
 3° 对角线法 以上我们通过比较,从通过
3° 对角线法 以上我们通过比较,从通过![]() 点的三个方向
点的三个方向![]() 的陡度挑出一个较陡的方向来,例如是
的陡度挑出一个较陡的方向来,例如是![]() ,但
,但![]() 并
并
不一定过![]() 点的最陡方向,其实只要利用过
点的最陡方向,其实只要利用过![]() 点的二个方向的陡
点的二个方向的陡
度就可以找出过![]() 点的更陡的方向来。
点的更陡的方向来。
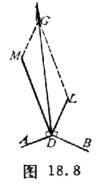
如图18.8,在过![]() 垂直于
垂直于![]() 的方向上取一点
的方向上取一点![]() ,使
,使![]()
的长等于![]() 到
到![]() 的陡度,且
的陡度,且![]() 和
和![]() 分别在
分别在![]() 的两侧;再在
的两侧;再在
过![]() 垂直于
垂直于![]() 的方向上取一点
的方向上取一点![]() ,使
,使![]() 的长等于
的长等于![]() 到
到
![]() 的陡度,且
的陡度,且![]() 和
和![]() 分别在
分别在![]() 的两侧,以
的两侧,以![]() ,
,![]() 为边
为边
作平行四边形,其对角线![]() 的方向就是在
的方向就是在![]() 点的陡度最大
点的陡度最大
的方向。
[步长加速法] 步长加速法实际上是瞎子爬山法和沿有利方向加速相结合的方法.其迭代程序如下:
(1) (1) 选取初始点(基点)![]() 和步长
和步长![]() ,命
,命![]() 。
。
(2) (2) 瞎子爬山(程序见瞎子爬山法)。
当沿各个坐标轴方向的局部探索都轮流进行后,这个阶段的局部探索也就完成了,下一步就可沿有利方向进行加速。
(3) (3) 加速爬山。命![]() 。若
。若![]() ,那末移到新的位置
,那末移到新的位置![]() 进行加速试探,
进行加速试探,
在此
![]()
有两种情形可能产生:
1° 如果![]() 的数值有改进,那末命
的数值有改进,那末命![]() ,应用步骤(2)的方法开始新的探索。
,应用步骤(2)的方法开始新的探索。
2° 如果![]() 的数值没有改进,那末取消这个加速,将基点放在上次发现的最好点,即
的数值没有改进,那末取消这个加速,将基点放在上次发现的最好点,即![]() 。命
。命![]() ,象步骤(2)一样开始一个新的局部探索。
,象步骤(2)一样开始一个新的局部探索。
如果经过一个阶段后发现![]() 不能加速移动,那末就缩小步长重复步骤(2)。如果逐次缩小步长都不能加速移动,这点便是最优点的近似解。
不能加速移动,那末就缩小步长重复步骤(2)。如果逐次缩小步长都不能加速移动,这点便是最优点的近似解。
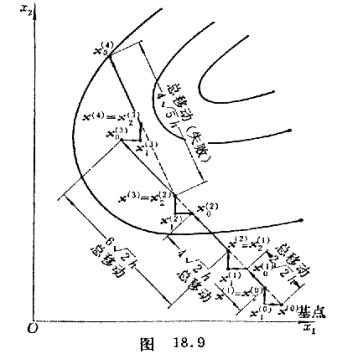 步长加速法在二维的情形如图18。9所示。
步长加速法在二维的情形如图18。9所示。
[方向加速法(共轭方向法)] 迭代程序如下:
(1) 从前面的最好数值位置![]() (可以是前一次迭代最后所确定的点或用其他方法所得的好点)和一组线性独立的探索方向
(可以是前一次迭代最后所确定的点或用其他方法所得的好点)和一组线性独立的探索方向![]() (可以取坐标轴的方向)出发。首先寻找过点
(可以取坐标轴的方向)出发。首先寻找过点![]() 平行于
平行于![]() 的直线上的最好点设为
的直线上的最好点设为![]() ,再找过点
,再找过点![]() 平行于
平行于![]() 的直线上的最好点设为
的直线上的最好点设为![]() ,继续这个过程直到所有n个探索方向都已试探过,最后所得点为
,继续这个过程直到所有n个探索方向都已试探过,最后所得点为![]() 。
。
(2) 寻找特殊点![]() ,这个点使目标函数的数值同前一点相比改进最大,即点
,这个点使目标函数的数值同前一点相比改进最大,即点![]() 给出
给出![]() 个移动的最大改变量
个移动的最大改变量![]() ,其中
,其中![]() 。此外决定矢量
。此外决定矢量![]() 。
。
(3) 计算![]()
(4) 记![]() 如果
如果
(1)
或
(2)
那末![]() 不是探索中的好方向,则应重新开始探索,从最后一点出发并用同样的方法,即
不是探索中的好方向,则应重新开始探索,从最后一点出发并用同样的方法,即![]() 和
和![]() ,重复步骤(1)。如果不等式(1),(2)都不满足,那末沿方向
,重复步骤(1)。如果不等式(1),(2)都不满足,那末沿方向![]() 探索直到找到极小点。将这个点定义为
探索直到找到极小点。将这个点定义为![]() ,而k+1阶段的新探索方向为
,而k+1阶段的新探索方向为![]()
![]() ;
;![]() ;又
;又![]() 。然后从步骤(1)出发重复整个过程,直到
。然后从步骤(1)出发重复整个过程,直到![]() ,其中
,其中![]() 为预先给定的允许误差。
为预先给定的允许误差。
例 应用方向加速法找出目标函数
![]()
的极小点。
解 应用导数的方法容易求出目标函数的绝对极小点为![]() 。下面用方向加速法来求出这个极小点。
。下面用方向加速法来求出这个极小点。
从点![]() 开始探索,探索方向用
开始探索,探索方向用![]() 和
和![]() 。
。
第一阶段 从基点出发,沿方向![]() 进行一维探索,移动距离由使
进行一维探索,移动距离由使
![]()
到达极小,得到![]() ,因此
,因此![]() ,而目标函数值由
,而目标函数值由![]() 减少到
减少到![]() 。再沿方向
。再沿方向![]() 用同样的方法探索,得到
用同样的方法探索,得到![]() ,同时
,同时![]() 。
。
为决定下一阶段是否用方向![]() ,应检验不等式(1),计算点
,应检验不等式(1),计算点![]() ,而
,而![]() ,由于
,由于![]()
![]() ,所以下一阶段不用方向
,所以下一阶段不用方向![]() 。
。
第二阶段 本阶段的方向和前一阶段的一样(因为![]() 不采用)。相继探索得到
不采用)。相继探索得到![]() ,而
,而 又
又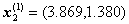 ,而
,而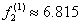 。再计算点
。再计算点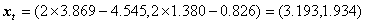 。在此
。在此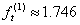 ,由于
,由于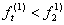 ,不等式(1)不满足。再检验不等式(2),计算
,不等式(1)不满足。再检验不等式(2),计算
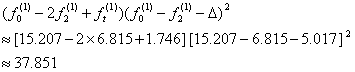
式中![]() 是目标函数在给定方向的最大改变量,即
是目标函数在给定方向的最大改变量,即![]() 。不等式(2)的右端是
。不等式(2)的右端是
![]()
因此不等式(2)不满足,即下一阶段可以采用方向![]()
![]() ,沿方向
,沿方向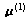 探索得到第三阶段的基点为
探索得到第三阶段的基点为![]() ,并且
,并且 。
。
第三阶段 本阶段的探索方向为![]() 和
和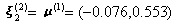 。沿这两个方向探索将发现不能再前进,因为事实上前一阶段已经找到绝对极小点。当然,这是不足为奇的,因为目标函数是二次的。
。沿这两个方向探索将发现不能再前进,因为事实上前一阶段已经找到绝对极小点。当然,这是不足为奇的,因为目标函数是二次的。
[方向步长双加速法] 迭代程序如下:
考虑第k阶段
(1) (1) 选择一初始点(基点)![]() ,一组步长
,一组步长 和一组方向
和一组方向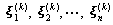 ,其中
,其中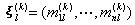 ,上指标
,上指标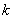 表示第
表示第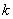 个阶段,下指标
个阶段,下指标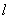 表示第
表示第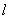 个方向。当
个方向。当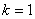 时,一般选择探索方向平行于坐标轴方向。
时,一般选择探索方向平行于坐标轴方向。
(2) (2) 依次平行于n个方向的每一个进行相继探索,若移动是成功的,则采用新点,若移动不成功则保留基点。若在一给定方向的移动是成功的,则下一次再在这个方向上探索时,步长将增大为![]() 倍
倍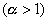 ;若失败,则缩小为
;若失败,则缩小为![]() 倍
倍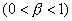 ,负号表示在反方向探索。一般取
,负号表示在反方向探索。一般取![]() 。
。
(3) (3) 直到在每一个方向上都至少有一次成功,一次失败,这时沿该方向的探索就告结束。依次沿平行于n个方向的探索完毕后最后一次成功的点为新的基点![]() 。下一阶段(即第
。下一阶段(即第![]() 阶段)的探索方向
阶段)的探索方向![]() ,由下列方程计算得到:
,由下列方程计算得到:
首先定义矢量
![]()
其中![]() 是在
是在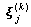 方向的所有成功移动的代数和,
方向的所有成功移动的代数和,
![]()
![]()
然后方向![]() 由下式给出
由下式给出
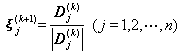
其中
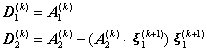
![]()
![]()
特别,其中主要方向

它的各个分量为
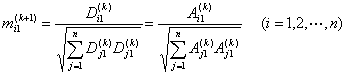
(4) (4) 以上步骤一直进行到![]() (
(![]() 为预先给定的允许误差)为止,所得最后的基点
为预先给定的允许误差)为止,所得最后的基点![]() 就近似于最优点。
就近似于最优点。
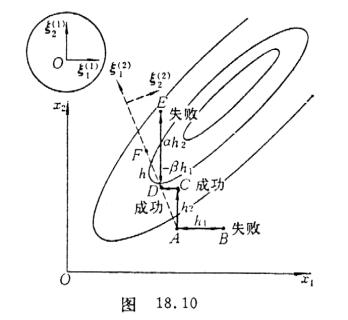 方向步长双加速法在二维的情况如图18.10所示。
方向步长双加速法在二维的情况如图18.10所示。
[单纯形调优法] 迭代程序如下:
(1) (1) 命n维空间的单纯形的n+1个顶点为![]() ,计算函数值
,计算函数值![]() ,比较大小,并确定
,比较大小,并确定
![]()
![]()
![]()
(2) (2) 求出最坏点![]() 的对称点
的对称点
![]()
式中 ![]()
(3) (3) 若![]() ,则将
,则将 缩小为
缩小为![]() ,
,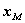 由下式定义:
由下式定义:
![]()
这里要求![]() ,是避免
,是避免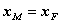 的情形发生。
的情形发生。
如果![]() ,那末
,那末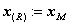 ,并重复以上步骤。
,并重复以上步骤。
如果![]() ,那末
,那末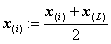 ,并重新开始迭代。
,并重新开始迭代。
(4) (4) 若![]() ,则将
,则将 扩大为
扩大为 ,
,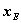 由下式定义:
由下式定义:
![]()
扩大的条件![]() 也可以换成
也可以换成
![]()
或 ![]()
如果上述条件满足,并且
![]()
那末 ![]()
否则 ![]()
并重复以上步骤。
上述过程一直继续到
![]()
或 ![]()
为止,其中![]() 是预先给定的正数。
是预先给定的正数。