二.不动边界的泛函的极值·欧拉方程
欧拉方程是泛函极值的必要条件,但不是充分的.在处理实际泛函极值问题时,一般不去考虑充分条件,而是从实际问题的性质出发,间接地判断泛函极值的存在性,直接利用欧拉方程来求出极值曲线.
![]() 假设F是二阶可微分的,函数y(x)是属于C2类的函数,并满足边界条件
假设F是二阶可微分的,函数y(x)是属于C2类的函数,并满足边界条件
y(x0)=y0, y(x1)=y1
极值曲线y(x)必须满足下面的微分方程(欧拉方程)
![]()
或
![]()
这是二阶微分方程,它的通解含有两个任意常数,由两个边界条件来确定.因此是一个两点边值问题.
1° 欧拉方程![]() 的可积类型
的可积类型
| 被 积 函 数 F | 欧 拉 方 程 |
| F不依赖于 | |
| F关于 | |
| F只依赖于 | |
| F依赖于x和 | |
| F只依赖于y和 | |
2° 极坐标系中的欧拉方程
| 泛 函 | 欧 拉 方 程 |
| | |
| | |
![]() 设函数
设函数
![]()
满足2n个边界条件:
![]()
欧拉方程为
![]()
假定其中出现的函数yi都是连续的,函数![]() 属于C2类,这个二阶微分方程组在
属于C2类,这个二阶微分方程组在![]() 空间中确定一族含有2n个参数的积分曲线,2n个参数应当由上面的2n个边界条件确定.
空间中确定一族含有2n个参数的积分曲线,2n个参数应当由上面的2n个边界条件确定.
![]() 假定F是n+2阶可微分的,函数y(x)属于C2n类,边界条件为
假定F是n+2阶可微分的,函数y(x)属于C2n类,边界条件为
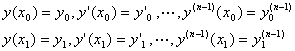
欧拉方程为
![]()
这个方程的通解含有2n个任意常数,这些常数一般可以由上面的2n个边界条件确定.
[多重积分的极值]
1° ![]() 型的泛函
型的泛函
假定函数F是三阶可微的,函数![]() 是二阶可微的,函数
是二阶可微的,函数![]() 在区域D的边界C上的值是给定的,欧拉方程为
在区域D的边界C上的值是给定的,欧拉方程为
![]()
式中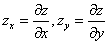 .这是一个二阶偏微分方程.
.这是一个二阶偏微分方程.
2° ![]() 型的泛函
型的泛函
欧拉方程为
![]()
式中
![]()
3° ![]() 型的泛函
型的泛函
欧拉方程为
![]()
式中 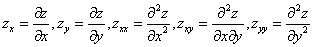
[用参数表示的泛函的极值] 考虑形如
![]()
的泛函,其中积分号下的函数不明显地含有自变量t,而且是对于![]() 及
及![]() 的一次齐次函数,即
的一次齐次函数,即
![]()
那末不管对参数t作任何替换,积分的形式总不改变.对于参数t的任何选择,函数![]() 及
及![]() 应满足两个欧拉方程的方程组:
应满足两个欧拉方程的方程组:
![]()
这些方程不明显地含有参数本身.但两个欧拉方程不是独立的,其中一个可由另一个推出.要想找出极值曲线,只要从两个欧拉方程中拿出一个来,把它跟确定参数的那个方程一起求积分.例如,若选择曲线弧长s作为参数,确定参数的方程为![]() .
.