二、常系数线性微分方程
1. 齐次线性微分方程通解的求法
[特征方程与特征根] 对于![]() 阶实常系数齐次线性微分方程
阶实常系数齐次线性微分方程
(2)
作相应的![]() 次代数方程
次代数方程
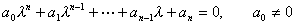 (3)
(3)称它为微分方程(2)的特征方程,特征方程(3)的![]() 个根
个根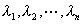 称为相应微分方程(2)的特征根.
称为相应微分方程(2)的特征根.
[齐次方程的通解] 为了求![]() 阶常系数齐次线性微分方程(2)的通解,只要找出它的
阶常系数齐次线性微分方程(2)的通解,只要找出它的![]() 个线性无关的特解就可以了.根据其全体特征根的各种情况,分别列出对应的线性无关特解.
个线性无关的特解就可以了.根据其全体特征根的各种情况,分别列出对应的线性无关特解.
| 特 征 根 | 对应的线性无关特解 |
|
| yj(x) = |
|
| y1(x) = y2(x) = |
|
| y1(x) = yr(x) = xr-1 |
|
|
|