和

                                                  (3)

都是奇异积分方程。

   2°  方程（1）的右边所定义的函数可以看作y(x)的傅立叶正弦变换。若当x>0时，F(x)逐段可微且存在，则方程（1）有唯一的反演公式：

  （x>0）

       考虑齐次积分方程          

                                                      (4)      

       从已知的公式

   (x>0,α>0)

可知确实是特征值。当时，对任意正常数α，函数

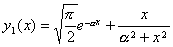    (x>0)

满足方程（4）；而当时，对任意正常数α，函数

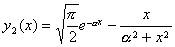    (x>0)

也满足方程（4）。于是这两个λ值是无穷重的特征值，即每个值对应无穷多个特征函数。这个事实与Fr方程的任一特征值只对应有限个独立特征函数是大不相同的。

   3°  由方程（2）右边所定义的函数F（x）是函数y（x）的拉普拉斯变换。因为不是一切函数都能作拉普拉斯变换，两个不同函数不能有同一个拉普拉斯变换。所以对一个给定函数F(x)，若（2）存在一个解，则解是唯一的。

考虑齐次积分方程

      （x>0）                     （5）

根据伽马函数的定义有

以代替a，得

由上面两等式推出

如果令

那末上式表明，函数

   （x>0）

是积分方程（5）的解。

因此，对参数a的任一值，有一个λ值对应，并且决定了方程（5）的一个非平凡解。

利用恒等式

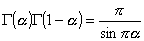
有

由此推出，在区间内的一切λ值都是奇异积分方程（5）的特征值。

    还能证明在区间内的一切λ值也是奇异积分方程（5）的特征值。

   积分方程（3）的积分区间是有限的，但是核是无界函数，这种奇异积分方程将在本节二和§3中考虑。