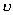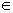二、 二、 一致空间
[复合关系与逆关系] 假设X是一个集,u和![]() 是X里的两个关系(即是u
是X里的两个关系(即是u![]() X´X,v
X´X,v![]() X´X),规定
X´X),规定
u![]()
![]() ={<x,y>|x
={<x,y>|x![]() X,y
X,y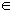 X,并且存在z
X,并且存在z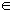 X,使
X,使
<x,z>![]() u并且<z,y>
u并且<z,y>![]()
![]() }
}
u![]()
![]() 当然也是X里的一个关系,称为u和
当然也是X里的一个关系,称为u和![]() 的复合关系.
的复合关系.
再规定
u-1 ={<x,y>|<y,x>![]() u},
u},
那末u -1也是X里的一个关系,称为u的逆关系.
容易证明
(u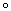
![]() )-1= V -1
)-1= V -1![]() u -1
u -1
[一致空间] 假定X是一个集,U是X里的一个不空的关系族(即U¹φ并且UÍX´X2),并且满足条件:
(i) 若u![]() U,则对任何x
U,则对任何x X,<x,x>
X,<x,x>![]() u;
u;
(ii) 若u![]() U,则存在
U,则存在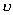
![]() U,使
U,使![]()
![]()
![]()
![]() u;
u;
(iii) 若u![]() U,
U,![]() 则u∩
则u∩![]()
![]() U;
U;
(iv) 若u![]() U,u
U,u
![]()
![]() X´X,则
X´X,则 ![]()
![]() U;
U;
(v) 若u![]() U,则u-1
U,则u-1![]() U .
U .
那末称U为X的一个一致性,<X,U>称为一致空间(有时称X是在U这个一致性下的一致空间).
把满足条件(i)—(iv)的U称为X的一个拟一致性,对应的<X,U>称为拟一致空间.
如果U和U'是集X的两个一致性,U![]() U',那末称U比U'粗,U'比U细.
U',那末称U比U'粗,U'比U细.
假定集X里有一个不空的关系族V,满足定义所说条件(i)和(ii),那末X的所有掩盖V的一致性的通集U0也是一个一致性,是能掩盖V的最粗的一致性,称为V所繁殖的一致性,V称为U0的一个亚基 U0存在
U0存在![]()
![]() V使
V使![]()
![]() u,那末称V为U0的一个基.
u,那末称V为U0的一个基.
对任何一个集X,由{{<x,x>|x![]() X}}所繁殖的一致性是最细的一致性.
X}}所繁殖的一致性是最细的一致性.
尺度空间可以看作一致空间的特例:假定X是一个尺度空间,把X里的关系族{{<x,y>|x和y的距离小于γ}|γ是一个正数}所繁殖的一致性称为由X的尺度产生的一致性.通常除特别声明外,一个尺度空间X总是看作在这个一致性下的一致空间.实际上,上面“γ是一个正数”的条件可以改作“γ是一个正有理数”(由于一致性的条件(iv)),所以由尺度产生的一致性一定有可数的基.
[一致拓扑与一致空间的尺度化] 假定<X,U>是一个一致空间.对x![]() X,u
X,u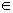 U,把{y|<x,y>
U,把{y|<x,y>![]() u}记作u[x],称为x的一个邻域.由所有这种邻域所繁殖的拓扑称为X的一致拓扑.以后如果不另外声明,一个一致空间X总是看作在一致拓扑下的拓扑空间.
u}记作u[x],称为x的一个邻域.由所有这种邻域所繁殖的拓扑称为X的一致拓扑.以后如果不另外声明,一个一致空间X总是看作在一致拓扑下的拓扑空间.
如果在一个一致空间里可以规定一个尺度,由这尺度产生的一致性跟原来的一致性相同,那末称这一致空间是可以尺度化.
一个一致空间可以尺度化的充分必要条件是:它的一致性有可数的基,并且它是T2空间.一个一致空间可以拟尺度化的充分必要条件是:它的一致性有可数的基.
[一致连续与一致同构变换] 假定<X,U>和<Y,V>是两个一致空间,f是一个把X变进Y的变换,如果对任何![]()
![]() V,总存在u
V,总存在u![]() U,使对所有的<x,y>
U,使对所有的<x,y>![]() u,<f(x),f(y)>
u,<f(x),f(y)>![]()
![]() 成立,那末称f为一致连续.一致连续必定连续,但是在一致拓扑下连续不一定一致连续.
成立,那末称f为一致连续.一致连续必定连续,但是在一致拓扑下连续不一定一致连续.
一个变上的可逆一致连续变换称为一致同构变换.一致同构变换一定是同胚变换,但是反过来说不一定对.
[一致收敛] 假定<Y,V>是一个一致空间,X是一个集,又假定<fp|p![]() Q>是XY里的一个点网,f
Q>是XY里的一个点网,f![]() XY ,如果对任何
XY ,如果对任何
![]() V,存在一个q
V,存在一个q![]() Q使对所有的p>q和所有的x
Q使对所有的p>q和所有的x![]() X,
X,
<fp(x),f(x)>![]() V
V
成立,那末称<fp|p![]() Q>一致收敛于f.
Q>一致收敛于f.
假定<Y,V>是一致空间,X是一个集,那末还可以对XY 规定一个一致收敛的一致性如下:对任何![]()
![]() V,可以得到XY 里的一个关系w
V,可以得到XY 里的一个关系w
w ={<f,g>|对所有的x![]() XX,<f(x),g(x)>
XX,<f(x),g(x)>![]()
![]() 成立}.
成立}.
所有这些w的全体所繁殖的一致性称为XY 的一致收敛的一致性.由这一致性所产生的拓扑称为XY 的一致收敛拓扑.可以看到,XY 里的一个点网一致收敛就是在一致收敛拓扑下收敛的意思.