2．多变量函数的极值
[极值(极大值或极小值)] 设函数
y= f (x1,x2,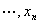
)= f (x)
定义于区域D中，且x0=(
)是这区域内的一点.
若点x0有一个邻域
0<|
|<δ,i=1,2,
使对于其中一切点，下面不等式成立：
f (x)<f (x0) ( 或f (x)>f (x0))
则称函数f (x)在点x0处有极大值（或极小值）.
[极值存在的必要条件] 假定函数f (x)在区域D内存在有限偏导数.若在点x0(∈D)处函数有极值，则必有
（2）
所以极值只能在使（2）式成立的点达到，这种点称为稳定点.
[极值存在的充分条件(二元函数的情形)] 设点x0=（
）为函数y= f (x1,x2)的稳定点，并且函数f (x1,x2)在稳定点x0的邻域内有定义，连续，并有一阶及二阶连续偏导数.引进记号
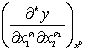，k = p1+p2
上指标“0”表示偏导数是在x0计算的.记
D1=
,D2=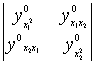
那末（i）稳定点x0是极小点的充分条件是：
D1>0 和 D2>0
即 
>0 和 
>0
（ii）稳定点x0是极大点的充分条件是：
D1<0 和 D2>0
即 
<0 和 
>0
若D2<0，则x0不是极值点，当D2=0时不能肯定x0是否极值点，必须考察更高阶的偏导数.
[极值存在的充分条件(一般情形)] 设点x0=(
)为函数y= f (x)= f (x1,x2,
)的稳定点，并且函数f (x)在稳定点x0的邻域内有定义，连续，并有一阶及二阶连续偏导数.引进记号
k =
上指标“0”表示偏导数是在x0计算的.定义行列式Di为
Di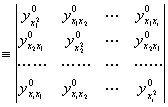
对n个变量依次计算n个行列式D1,D2,…,Dn.那末
（i）稳定点x0是极小点的充分条件是：所有的行列式都是正的，即
Di>0, i=1,2,
（ii）稳定点x0是极大点的充分条件是：所有标号为偶数的行列式是正的，所有标号为奇数的行列式是负的，即
Di<0, i=1,3,
Di>0, i=2,4,
如果上列两条件都不满足，那末稳定点可以不是极值点.如果所有的Di都是零，就必须考察更高阶的偏导数.