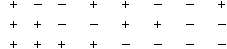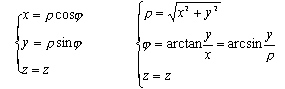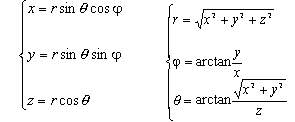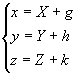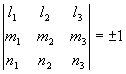二、空间坐标系及其变换表
| 坐 标 系 与 图 形 | 公 式 与 说 明 | |||||
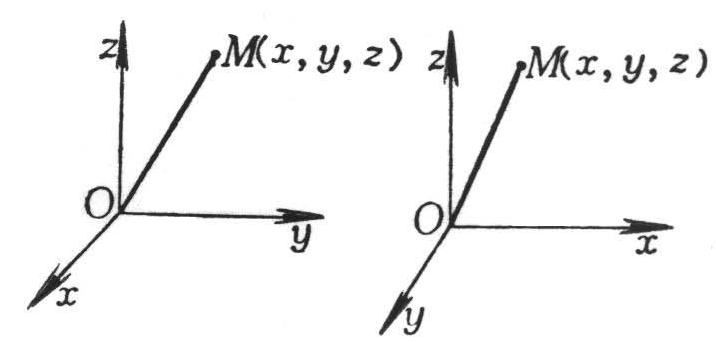
| [笛卡儿直角坐标系]
(c) | Ox为横轴,Oy为纵轴,Oz为竖轴 M(x, y, z)
| |||||
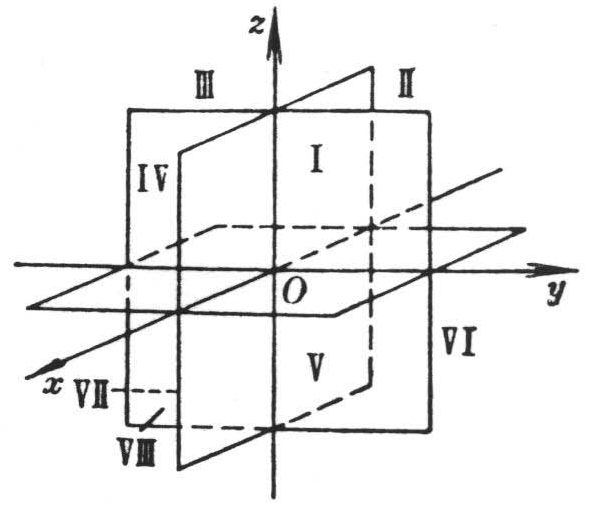
| 卦限 |
| |||||
x y z | | |||||
|
| ||||||
| 坐 标 系 与 图 形 | 公 式 与 说 明 | |||||
| [圆柱面坐标系]
| r ,j 为点M在Oxy平面上投影的极坐标,z为点M到Oxy平面的距离.这里 0 £ r < ¥ -¥ < j < ¥ -¥ < z < ¥ | |||||
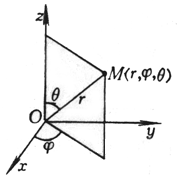
| [球面坐标系(极坐标系)]
| r为矢径长(OM),j 为经度,q 为纬度(或极距角) 这里 0 £ r < ¥ - ¥ < j < ¥ 0 £ q £ p | |||||
| [圆柱面坐标与直角坐标的互换] |
| |||||
| [球面坐标与直角坐标的互换] |
| |||||
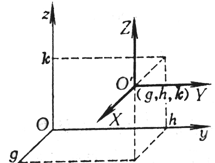
| [坐标轴的平移]
|
式中x, y, z为旧坐标;X, Y, Z为新坐标;g, h, k为新坐标系原点O¢ 在旧坐标系内的坐标 | |||||
| [坐标轴的旋转]
| 按下表给出新坐标轴OX,OY,OZ的方向余弦时 | |||||
|
| 新坐标轴 | 方向余弦 (见§ 4) |
| |||
| OX OY OZ | l1 m1 n1 l2 m2 n2 l3 m3 n3 | |||||
| 则有
| ||||||
[欧拉角] 新坐标轴的位置也可以用三个所谓欧拉角来确定(见上图):
- 章动角q 为OZ与Oz两轴正向夹角(0£ q < p ).
- 进动角y 为OA与Ox的夹角(0£ y < 2p ),OA为OXY与Oxy两平面的交线,面对Oz轴的正向,y 按逆时针方向从Ox轴开始计算.
- 自转角j 为OA与OX的夹角(0£ j < 2p ),面对OZ轴正向,j 按逆时针方向从OX轴开始计算
若设c1=cosθ, c2=cosy , c3=cosj
s1=sinθ, s2=siny , s3=sinj
变换行列式 Δ=