2. 多变量函数的泰勒公式
[泰勒公式] 假定在某一点(x0,y0)的邻域D内二元函数f(x,y)有直到n+1阶为止的一切连续偏导数.分别给x及y以改变量h及k,使连结点(x0,y0)及(x0+h,y0+k)的直线段不越出D外,那末f (x,y)在D内可表成形式:
1° f (x0+h,y0+k)
=
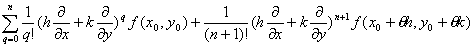
(0<θ<1)
式中符号
的意义如下:把
,
看作一个数(而不是看作微分运算的符号),并根据二项公式展开,得到
=
=
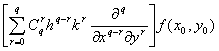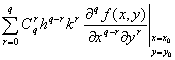
20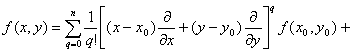 
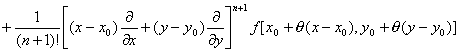
特别,当x0=0,y0=0时,得到
[马克劳林公式]
f (x,y)=
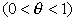
对二元以上的多变量函数有类似的公式.
[泰勒级数] 在上面泰勒公式2°中,如果把展开式进行到(
)和(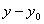
)的任意高的乘幂,则有
f (x,y)=
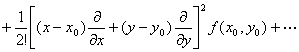
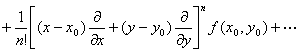
不论它是否收敛,以及它的和是否等于f(x,y),都称它为f(x,y)的泰勒级数.
[马克劳林级数] 在上面马克劳林公式中,如果把展开式进行到x,y的任意高的乘幂,则有
f (x,y)=f (0,0)+
不论它是否收敛,以及它的和是否等于f (x,y),都称它为f (x,y)的马克劳林级数.