五.变分问题的直接方法

[欧拉有限差分法]  考虑泛函

的极值，边界条件为

其步骤如下：

(1)    (1)      将积分区间分成n+1等份（图18.11）,分点为

又.这时

式中

(2)    (2)      选取使函数达到极值，也就是由方程组

来确定.如果从这个方程组难于确定时，也可用本章§2,§3的方法.于是可以用所得到的折线表示变分问题的近似解.

区间[a,b]分得愈细所得近似解就愈精确.

[里兹法]  考虑泛函

的极值，边界条件为

其步骤如下：

(1)    (1)      选择一适当的函数序列（称为坐标函数）：

构造函数

式中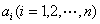为待定常数.将的近似值代入泛函的表达式，则

(2)    (2)      选取,使函数达到极值，也就是由方程组

来确定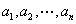.如果从这个方程组难于确定时，也可用本章§2,§3的方法.于是可以得到变分问题的近似解.

当n越大时所得近似解就愈精确.

里兹方法也适用于泛函和依赖于多个函数的泛函.

例 求泛函

的极值，其中积分域D为椭圆.

解  只取一个坐标函数xy，则得

,

这时从

得到

而极值问题的近似解为

[康特罗维奇法]  考虑泛函

                 (1)

的极值，它展布在由二曲线,和二直线所围成的区域D上(图18.12).设在区域D的边界上函数的值z(x, y)已经给出.其步骤如下：

(1)    (1)      选取坐标函数序列：

构造函数

式中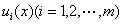是待定函数.将z(x, y)的近似表达式

代入(1)式得

即

(2)    (2)      选取函数使泛函达到极值，也就是由欧拉方程

来确定.而任意常数的选取是使在直线和上满足所给的边界条件.于是可以得到变分问题的近似解.

康特罗维奇法也适用于其他形式的泛函.

说明   一般说来，用同样的坐标函数以及相同的项数m，康特罗维奇法比里兹法精确.因为以变量为系数的函数类

较之以常数为系数的函数类

更为广阔.