二、在弹性力学问题上的应用（位移法）
弹性体Ω在荷载f（作用于Ω内的体力），q（作用于边界
上的面力）等作用下引起小变形，其变形能可表示为
式中{ε}，{σ}分别表示应变、应力各分量排成的列矢量（§5），它们与位移u的线性关系形式上可写成
{ε}=Bu {σ}=
DBu
B是微分算子矩阵，D是与弹性系数E,
有关的对称矩阵，视问题的性质而定.于是，弹性体的总势能即变形能与外力势能之和，为u的二次泛函：
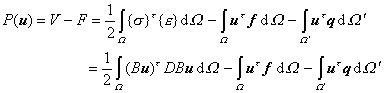
最小势能原理指出，对满足边界上一定约束条件的所有位移中，以保持力的平衡状态的位移所造成的总势能达到最小值.利用矩阵D的对称性，可知位移函数u就是变分方程
的解,把Ω划分为有限个单元
，其节点i的参数值为{u}
，并假定在
上u（各分量）的插值函数可表示为同类型的多项式：
（1）
它称为位移模式，式中
表示对单元
的各节点求和，
为坐标变量的多项式，随单元的形状与插值的方式而定（即§2~§4中所列的各种型函数），而对角线分块矩阵
的行、列数与u的分量个数有关，例如，对空间问题
为3
3r（r表示每个分量的节点参数值的个数）矩阵.
把（1）代入
，得
(2)
设
(3)
(4)
(5)
(6) 式中
表示对所有含节点i的单元求和.
表示对所有含i，j两个节点的单元求和，当i，j两个节点不在同一个单元时，
；j 也可取i，这时
=
；其余情况，可能对一个或几个单元求和，视区域划分方式而定.
这些系数的力学意义是很明显的：
表示在位移模式（1）的假定下，由于节点j(包括i节点本身)具有位移、转动等等变形值
通过弹性体单元
的作用而在节点i产生的反力*.
就是通常所谓单元的刚度矩阵；虽然包括i、j两个节点的单元个数有各种可能，但依定义(4)可知
，就是由于节点j的变形值而引起节点i上的反力.对于整个区域的节点j（实际上只有与节点i邻近的几个节点）求和，就得出由于变形而产生节点i上的总反力.同样，(5)(6)右端的积分分别表示体力、面力等外荷载按位移模式(1)通过单元
而分配给第i节点的相应的外力*，简称为在单元
上荷载的等价节点力，而其和
则是整个区域荷载分配给节点i的总外力.从(2)提出
得到
(7)
除了在给定位移的部分边界(在这部分就不给定面力q)上有关的节点参数值(其变分已等于零!)外，由于各个变分
的相互独立性，圆括号内各分量(变分为零的部分除外)都应等于零.这正反映出处于平衡状态时，任一非约束节点的反力与外力之和等于零,亦即力在各节点应取得平衡这一客观事实.
最后，按整个区域的节点编号,依序排列待定的节点参数值,除去已加约束的那一部分，从而构成一个总的节点参数值列矢量
,对
,
也划掉相应的行、列,从而构成总的系数矩阵,即所谓总刚度矩阵
(撇号表示已做划行、划列的处理)与右端列矢量
,于是(7)可写成
由于定义(3)与D的对称性，单元的
，而依(4),
，即
,把其中第m行、第m列划掉后也是对称的，因此，经过划行、划列处理的K是对称的;当区域细分后,大量的第j节点与第i节点不在同一个单元上，则大量的
,这表明K是稀疏的.这种对称性与稀疏性正是改进计算方法与提高解题速度的主要根据.