第二十章                        第二十章       初等数论

    本章简要地介绍了初等数论的基础知识.共分六节.前五节讨论了整数的性质与辗转相除法,连分数与费波那奇序列,同余式与孙子定理,介绍了几种重要的数论函数和麦比乌斯变换,并列出几类不可约多项式的判别方法.最后一节对代数数等基本概念和性质作了简单的介绍.

§1    整数

    [整数部分与分数部分] 设a 为一实数,不超过a 的最大整数称为α 的整数部分,记作.而称为a 的分数部分.

    例如  ,,等等

    整数部分具有下列关系式:

           ,n为自然数

           ，n为自然数

            或

    注意,在计算机程序中的“取整运算”与这里的“整数部分”意义是有差别的:当时是一致的;当时不一致,例如,但计算机上取整后为.

    [整除性]  若有一整数c,使得整数a与b之间适合于

    则称b可整除a,记作。这时a称为b的倍数,b称为a的因数(或约数).

若b不能整除a,则记作ba.

    整除性具有下列性质(下列各式):

    1°  若,, 则;

    2°  若, 则;

    3°  若,,则对于任意整数m,n有

    4°  若b是a的真因数(即),则

    [素数与爱拉托斯散筛法] 恰有1和本身两个自然数为其因数的大于1的整数称为素数,记作.除2为偶素数外,其余素数都是奇数.

    素数具有性质:

    1°  素数有无限多个. 如果不超过自然数n的素数个数记作 p(n),则当时,有*,进一步有

    2°  设p为素数,若,则或.

    3°  中含素数p的方次数等于

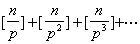
    4°  若为正整数,它不能被不超过的所有素数所整除,则n必为素数.这种判别自然数是否为素数的方法称为爱拉托斯散筛法.由此法可建立素数表.

    [唯一分解定理]  大于1的自然数都可唯一地分解为素数幂的积.设,为自然数,则n可唯一地表为

            (为自然数)

              (为素数)

这称为n的标准分解式。n所含不同素因数的个数s不超过.

    显然,任意自然数n可表为

                 (k,m 为自然数或零)

这种表达式是唯一的.

    [麦森数]  整数

                 ( p为素数)

为素数者称为麦森数.至今仅发现27个,即

是否有无穷个麦森数还未证明.

    [费马数]  整数

                   (n为自然数)

称为费马数.至今只发现5个费马数为素数,即

下列46个费马数皆非素数:

    [辗转相除法*] 每一个整数a可以唯一地通过正整数b表为

式中q称为a被b除所得的不完全商,r称为a被b除所得的余数.辗转相除法是指下列一串有限个等式:

                              (1 )

    例1  设a=525 ,b=231 ,根据(1)式可列出下面的算式和草式:

          算    式              草    式

    [最大公因数与最小公倍数]  设a,b为整数.既能整除a,又能整除b的正整数称为a,b的公因数,其最大者称为a,b的最大公因数*,记作,即

特别当时,称a,b互素.

    设a,b为正整数.a,b都能整除的正整数称为a,b的公倍数,其最小者称为a,b的最小公倍数*,记作,即

    设为n个正整数,用归纳法定义其最大公因数为

其最小公倍数为

    最大公因数与最小公倍数具有下列性质:

    1° 存在整数x,y,使得.并可由辗转相除法具体求出x,y.也由辗转相除法的一串等式得到,即

    例2  由例1得(525,231)=21.因为由例1的算式有

所以得到 x=4,y=－9.

    2° 对任意二整数x,y,必有.

    3° 若,,则.

    4° 若则

      若,则

    5° 若a,b为二正整数,为它们的素因数,且标准分解式分别为

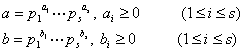
则

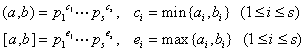
    6°

    7° 若为互素的正整数,即,则